
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
PART C AND D ONLY
Transcribed Image Text:SC
600
500
400
N
300
!
200
100
1
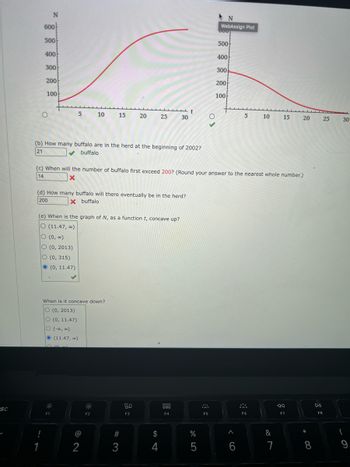
(b) How many buffalo are in the herd at the beginning of 2002?
21
✔ buffalo
(d) How many buffalo will there eventually be in the herd?
200
X buffalo
(e) When is the graph of N, as a function t, concave up?
O (11.47, ∞)
O (0, ∞)
O (0, 2013)
O (0, 315)
5 10 15 20 25
(0, 11.47)
:0
F1
When is it concave down?
O (0, 2013)
O (0, 11.47)
O (-∞0, ∞0)
(11.47, ∞)
(c) When will the number of buffalo first exceed 200? (Round your answer to the nearest whole number.)
14
X
@
2
F2
#3
30
20
F3
$
4
t
000
000
F4
%
5
O
F5
AN
WebAssign Plot
000
500
400
300
200
1000
A
5
6
10
F6
&
15
7
Aa
F7
20 25
*
8
DII
F8
30
9
Transcribed Image Text:b
lock
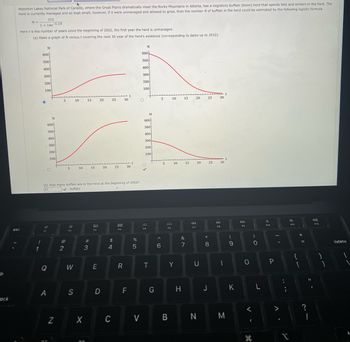
Waterton Lakes National Park of Canada, where the Great Plains dramatically meet the Rocky Mountains in Alberta, has a migratory buffalo (bison) herd that spends falls and winters in the Park. The
herd is currently managed and so kept small; however, if it were unmanaged and allowed to grow, then the number N of buffalo in the herd could be estimated by the following logistic formula.
315
1+14e-0.23t
esc
N=
Here t is the number of years since the beginning of 2002, the first year the herd is unmanaged.
(a) Make a graph of N versus t covering the next 30 year of the herd's existence (corresponding to dates up to 2032).
!
1
N
600
500
400
300
200
100
F1
600
500
400
300
200
100
O
A
N
Q
5
N
(b) How many buffalo are in the herd at the beginning of 2002?
21
✓buffalo
2
5 10 15 20 25
-0
F2
t
10 15 20 25 30
W
S
X
#3
80
F3
E
D
$
4
C
9.00
DOD
F4
R
30
LL
t
F
27 2
%
N
600
500
400
300
200
100
O
V
N
600
500
400
300
200
100
F5
T
G
< 6
5
5
F6
B
10
10
Y
15
H
15
&
7
20
Ja
F7
20
U
▬▬▬▬†
ML
25
* 00
25 30
8
J
30
DII
F8
1
N M
(
9
K
DD
F9
O
<
)
0
L
J
F10
P
A
I
()
F11
{
[
+11
(1)
F12
}
1
)
delete
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Similar questions
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

