AY E | Figure Q1 X
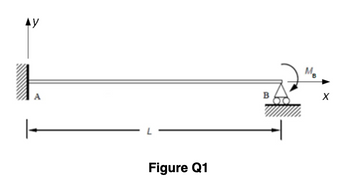
A propped cantilever beam is loaded by a bending moment of the magnitude M_B at the point B as shown in Figure Q1. The cross-section of the beam is a rectangle of the width w and the hight ℎ that are constant along the length of the beam L. The beam material’s Young’s modulus is Q.
Assuming the positive deflections and positive vertical reaction forces are upward, calculate
-
- the value of the reaction forces at points A and B
- the absolute value of the reaction bending moment at point A
A) Let R represent the reaction force at Support B. By releasing the beam at Support B and imposing a force R at Point B, the deflection of the beam consists of two parts,i.e.
Part I- the deflection caused by M_B ;
Part II- the deflection caused by R
Please treat R, w, h , L , E as variables in this step , the mathematical equation for the deflection at Point B caused by R ( Part II) can be written as:
b)
Using the provided data:
- cross-section width w = 14 mm,
- cross-section hight h = 82 mm,
- length of the beam L =2 m ,
- beam material’s Young’s modulus Q =233 GPa,
- applied bending moment M_B = 9 kN.m
The value of the deflection at Point B caused by M_B ( Part I) can be calculated as: __mm
c)
Based on the given values of dimensions and material parameters,
- the value of R can be calculated as __ kN;
- the value of the vertical reaction force at Support A can be calculated as __ kN;
- the value of the horizontal reaction force at Support A can be calculated as __ kN
- the absolute value of the reaction moment at Support A can be calculated as __ kN.m
Step by step
Solved in 4 steps with 4 images
