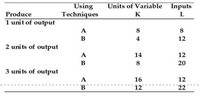
Assuming the price of labor (L) is $5 per unit and the price of capital (K) is $10 per unit, what production technique should this firm use to produce 2 units of output?  1.2) Assume the price of labor (L) is $5 per unit, the price of capital (K) is $10 per unit, and that firms attempt to minimize costs. The total variable cost of producing one unit of output is. Show Calculation   1.3) Refer to Table 8.1. Assume that the relevant time period is the short run. Assuming the price of labor (L) is $5 per unit and the price of capital (K) is $10 per unit, the average variable cost of producing two units of output is. Show Calculation   1.4) Refer to Table 8.1. Assume the price of labor (L) is $5 per unit, the price of capital (K) is $10 per unit, and that firms attempt to minimize costs. The marginal cost of producing the third unit of output is. Show Calculation

Suppose that the production function for Hannah and Sam's home remodeling business is            Q = F(L,K)            Q = 10L0.1K0.4.Assume the wage rate is $8,000 per week and the cost of renting a unit of capital is $1,000 per week.a. What is the least-cost input combination for remodeling 400 square feet each week?      Instructions: Round your answers to 2 decimal places.      units of labor and  units of capital.  b. What is the total cost?         Instructions: Round your answer to 2 decimal places.    $  .revised jrl 08-11-2011

a. A firm's long-run total cost can be written as LTC = 3000Q - 50Q2 + (1/3)Q3 and its long-run marginal cost by LMC = 3000 - 100Q + Q2. Find the range over which the firm will experience economies of scale. Explain your answer. b. A firm has a production function of Q = K * L + L, where the marginal product of labor is  MPL = K + 1 and the marginal product of capital is MPK = L. The wage rate (W) is $100 per worker and the rental price (R) is $100 per unit of capital. In the short-run, capital (K) is fixed at 4. Find the minimum total cost of production in the short- and long-run if the firm produces 100 units of output.

4. Ikea Inc., a home remodeling business. The number of square feet they can remodel in a day is described by the Cobb-Douglas production function Q= F (L,K)= 4K5L0.5 where L is their number of workers and K is units of capital. The wage rate is $5 a day, and a unit of capital costs $20 a day. What is their minimum cost input combination for remodeling (Q=200) 200 square feet a day? What is the total minimum cost level? (15p)

A firm has a fixed production cost of $4000. For the first 100 units of production, the firm has a marginal cost of $50 per unit produced. Producing more than 100 units has a marginal cost of $70 per unit produced. The firm cannot produce more than 150 units. How much does it cost to produce at q=0? at  q=50? at q=100? at q=125? at q=150? Graph the firm’s marginal cost function

Emma sells hot chocolate outside of Yankees baseball games. They have two inputs in the production of hot chocolate: (hot chocolate mix (x1, measured in kg) and labour (x2, measured in hours. The production function for hot chocolate (in liters) is: f (x1 , x2) = (x1)1/3(x2)1/3 A) Does this firm have constant, increasing or decreasing returns to scale? The cost of hot chocolate mix is w1, and the cost of labour is w2. If Emma produces "y" liters of hot chocolate the cheapest way possible, then B) How many kilograms of hot chocolate mix would they use? C) How many hours of labour? D) What is the cost function of producing this much hot chocolate?

A firm estimates its production function as Q = -2.4 + 20*L -.5*L2 + 30*K -1.00*K2 + 15*F -.3*F2. Total cost is TC = $2*L + $2.5*K + $1.75*F.  The firm wishes to produce 400 units of output.  Use Excel to find the cost minimizing amounts of L, K and F. How much F (Fuel) should the firm use?

Suppose w= 1 and r= 3. Solve the cost minimization problem to find L*(q) and K*(q). Then find the cost function C(q).

Suppose that the Acme Gumball Company has a fixed proportions production function that requires it to use two gumball presses and one worker to produce 1,000 gumballs per hour. a. Explain why the cost per hour of producing 1,000 gumballs is 2v + w (where v is the hourly rent for gumball presses and w is the hourly wage). b. Assume Acme can produce any number of gumballs they want using this technology. Explain why the cost function in this case would be TC = q(2v +w), where q is output of gumballs per hour, measured in thousands of gumballs. c. What is the average and marginal cost of gumball production (again, measure output in thousands of gumballs)? (show the complete formula) Draw the graph for the average and marginal cost curves for gumballs assuming v=3, w-5 (show working) Now draw the graph for these curves for  v=6, w=5.( show working) Explain why these curves have shifted.

Consider the following short run cost function: TC = 4Q³ - 24Q² + 16Q + 100 Derive the expressions for marginal cost and average total cost. What can we infer about the range of output over which production shows increasing returns to labor and diminishing returns to labor?