MATLAB: An Introduction with Applications
MATLAB: An Introduction with Applications
6th Edition
ISBN: 9781119256830
Author: Amos Gilat
Publisher: John Wiley & Sons Inc
Bartleby Related Questions Icon

Related questions

Q: Suppose that an electronics store runs a promotion. At the cash register, each separate item is…
A:
Q: Given P(A) = 0.052, P(B) = 0.045, and P(C) = 0.149, and that events A, B, and C are mutually…
A:
Q: Q14. A red and a blue die are thrown. Both dice are fair. The events A and B are defined as follows:…
A:
Q: Hello. I appreciate any help. Thanks.
A: Given two events A and B, P(A) = 0.2P(B) = 0.3P(A U B) = 0.4P(A ∩ B) is the probability of event A…
Q: Consider two events, A and B, such that P(A) = 0.60, P(B) = 0.35, and P(A and B) = 0.25. Are events…
A: Consider the two events A and B. PA=0.60 PB=0.35 PA∩B=0.25
Q: Consider two independent events A and B.Suppose it is known that P(A)=0.27 and P(A or B)=0.5474.…
A:
Q: OA. 0.12 B. 0.4 C. 0.8 O D.0
A: For two events, A and B, The general formula for probability is as: P(A or B)=P(A)+P(B)-P(A∩B). If…
Q: Given P(A) = 0.150, P(B) = 0.172, and P(C) = 0.185, and that events A, B, and C are mutually…
A: here given, P(A)=0.150, P(B)=0.172 P(C)=0.185   A,B and C are mutually exclusive event. so, P(A and…
Q: If events A and B are independent and P(A)= 0.32, P(B)= 0.28 Calculate P(A and B)? Round to…
A: Answer: From the given data, P(A) = 0.32  and  P(B) = 0.28 If events A and B are independent events
Q: You are given two events C and B. You want to determine if the events are mutually exclusive…
A: Determine whether the events C and B are mutually exclusive or not.   The correct option is…
Q: Given that A and B are two mutually exclusive events, find  P(A or B) for the following. P(A) =…
A:
Q: ven P(A) = and P(B) = ³ Find P(A or B), if A and B are mutually clusive events.
A:
Q: Suppose that A, B are two independent events, with P(A) = .1 and P(B) = .2. Find P(A|B).
A:
Q: In each of Exercises, decide whether or not the two events in question are independent or whether it…
A:
Q: Given P(A) = 0.104, P(B) = 0.049, and P(C) = 0.058, and that events A, B, and C are mutually…
A: Given P(A) = 0.104, P(B) = 0.049, and P(C) = 0.058, and that events A, B, and C are mutually…
Q: The events A and B are mutually exclusive. If P(A) = .33 and P ( B) = .26, what is the P( A or B)
A: Given that  P(A) = .33 and P ( B) = .26
Q: If P(A) = 0.30, P(B) = 0.20, P(A and B) = 0.09, what can be said about events A and B? Events A & B…
A: It is given that, P(A) = 0.30, P(B) = 0.20 and P(A and B) = 0.09.
Q: If A and B are independent events with P(A)=0.9 and P(B)=0.8, find P(A AND B).
A: It is given that , A and B are the two independent events & their probabilities is P(A) = 0.9…
Q: The events A and B are mutually exclusive. If P(A) = .31 and P ( B) = .42, what is the P( A or B)
A: It is given that  P(A) = 0.31 P(B) = 0.42
Q: P(A) = 0.6 P(B) = 0.5 P(A|B) = 0.42 P(A) = 0.3 P(B) = 0.5 P(A|B) = 0.3 P(A) = 0.45 P(B) = 0.75 P(A…
A: Determine if events A and B are independent for given problems
Q: The events A and B are mutually exclusive. If P(A) = 0.3 and P(B) = 0.6, what is P(A or B)? O A. 0.9…
A: Given Data: P(A)=0.3 P(B)=0.6   A and B are mutually exclusive events
Q: Suppose that E and F are two events and that P(E)=0.8 and P(F|E)=0.5. What is P(E and F)​?
A: Given data,  P(E)=0.8  P(F|E)=0.5 P(E and F)​=?
Q: Suppose that AA and BB are two independent events for which P(A)=0.18 and P(B)=0.8 . Find each of…
A: Two events A and B are said to be independent if; P(A and B)=P(A)×P(B)
Q: Given P(A) = 0.076, P(B) = 0.184, and P(C) = 0.159, and that events A, B, and C are mutually…
A: Solution: Mutually exclusive events: Two events A, B and C are said to be mutually exclusive when…
Q: The events A and B are mutually exclusive. If ​P(A)=0.6 and ​P(B)=0.2​, what is​ P(A or​ B)?
A:
Q: Given P(A) = 0.63, P(B) = 0.27, and the fact that events A and B are independent, What is P(A and…
A: Formula : P(A and B) = P(A) * P(B)
Question
Assume that we have two events, \( A \) and \( B \), that are mutually exclusive. Assume further that we know \( P(A) = 0.70 \) and \( P(B) = 0.30 \). If an amount is zero, enter “0”. a. What is \( P(A \cap B) \)? [Input box] b. What is \( P(A|B) \)? [Input box] c. A student in statistics argues that the concepts of mutually exclusive events and independent events are really the same, and that if events are mutually exclusive they must be independent. Do you agree with this statement? Use the probability information in this problem to justify your answer. - [Dropdown] - because \( P(A|B) \) - [Dropdown] - \( P(A) \). d. What general conclusion would you make about mutually exclusive and independent events given the results of this problem? - [Dropdown]
expand button
Transcribed Image Text:Assume that we have two events, \( A \) and \( B \), that are mutually exclusive. Assume further that we know \( P(A) = 0.70 \) and \( P(B) = 0.30 \). If an amount is zero, enter “0”. a. What is \( P(A \cap B) \)? [Input box] b. What is \( P(A|B) \)? [Input box] c. A student in statistics argues that the concepts of mutually exclusive events and independent events are really the same, and that if events are mutually exclusive they must be independent. Do you agree with this statement? Use the probability information in this problem to justify your answer. - [Dropdown] - because \( P(A|B) \) - [Dropdown] - \( P(A) \). d. What general conclusion would you make about mutually exclusive and independent events given the results of this problem? - [Dropdown]
Expert Solution
Check Mark
Step 1: Define the terms independent and mutually exclusive events.

Since you have posted a question with multiple sub-parts, we will solve first three sub-

parts for you. To get remaining sub-part solved please repost the complete question and

mention the sub-parts to be solved.


Independent events: 

Let A and B be any two events are said to be independent if,

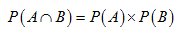
Statistics homework question answer, step 1, image 1

Mutually exclusive events: 

The two events are said to be mutually exclusive events if,

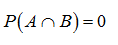
Statistics homework question answer, step 1, image 2

bartleby

Step by stepSolved in 5 steps with 3 images

See solution
Check out a sample Q&A here
Blurred answer
Knowledge Booster
Background pattern image
Similar questions
Recommended textbooks for you
Text book image
MATLAB: An Introduction with Applications
Statistics
ISBN:9781119256830
Author:Amos Gilat
Publisher:John Wiley & Sons Inc
Text book image
Probability and Statistics for Engineering and th...
Statistics
ISBN:9781305251809
Author:Jay L. Devore
Publisher:Cengage Learning
Text book image
Statistics for The Behavioral Sciences (MindTap C...
Statistics
ISBN:9781305504912
Author:Frederick J Gravetter, Larry B. Wallnau
Publisher:Cengage Learning
Text book image
Elementary Statistics: Picturing the World (7th E...
Statistics
ISBN:9780134683416
Author:Ron Larson, Betsy Farber
Publisher:PEARSON
Text book image
The Basic Practice of Statistics
Statistics
ISBN:9781319042578
Author:David S. Moore, William I. Notz, Michael A. Fligner
Publisher:W. H. Freeman
Text book image
Introduction to the Practice of Statistics
Statistics
ISBN:9781319013387
Author:David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:W. H. Freeman
SEE MORE TEXTBOOKS