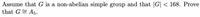
Assume that G is a non-abelian simple group and that |G| < 168. Prove that G = A5.

If f: G, → G2 is a grouphomomorphisim. Then if G, is cyclic then f(G2) is Select one: а. сyclic b. not abelian c. empty set

Decide if the abelian group Z/2 × Z/2 is cyclic or not. Prove your answer

Define * on Z by r * y = x + y + 4. Then: (a) Prove that * is a binary operation on Z. (b) Show that * is an associative operation on Z. (c) Determine the identity element for * in Z. (d) Show that every element of Z is invertible with respect to *. (e) Prove that (Z, *) is an abelian group.

Let (G,*) and (H,*) be finite abelian groups. If G x G = H x H then G=H. Show that they are isomorphic by giving the necessary isomorphism.

Prove that exactly one of the non-abelian groups of order 8 is isomorphic to a semidirect product C4 x C₂, explicitly identifying which one it is.

Prove that if G/Z(G) is cyclic, then G is abelian.

Determine whether U(12) with multiplication mod 12 is a cyclic group or not.