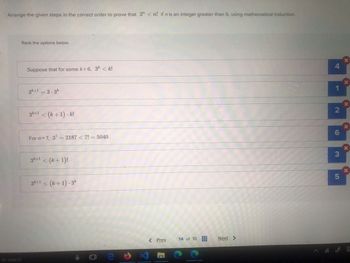
Please help me with this two questions. I am having trouble understanding why the answers are incorrect and what the correct answer is. Please provide the correct answer to the following 2 questions belowThank you Arrange the given steps in the correct order to prove that 3" 6, 3k E Click and drag the steps in the correct order to show that 3 divides n³ + 2n whenever n is a positive integer using mathematicalinduction.BASIS STEP:31 (13+2 1), i.e., 3 | 3, so the basis step is true.INDUCTIVE STEP:Suppose that 3 | (k³ + 2k).By the inductive hypothesis, 3 | (k³ + 2k), andcertainly 3 | 3(k² + 1).As the sum of two multiples of 3 is again divisibleby 3, 3 | ((k+1)3 + 2(k + 1)).31 (03+2 0), i.e., 3 | 0, so the basis step is true.(k+1)3 + 2(k + 1) = (k³ + 3k² + 1) + (2k + 2) = (k³ +2k) + 3(k² + 1)(k+1)3 + 2(k+1) = (k³ + 3k² + 1) + (2k + 2) = (k³ +2k) + 3(k² + 1)Suppose that 3 | (k³ + 2k).By the inductive hypothesis, 3 | (k³ + 2k), andcertainly 3 | 3(k² + k + 1).As the sum of two multiples of 3 is again divisibleby 3, 3 | ((k+1)3 + 2(k + 1)).(k+1)3 + 2(k+1) = (k³ + 3k² + 3k+ 1) + (2k + 2) =(k3 + 2k)+3(k² + k + 1)By the inductive hypothesis, 3 | (k³ + 2k), andcertainly 3 | 3(k² + k + 1).31 (13+2 1), i.e., 3 | 3, so the basis step is true.

Answered: Image /qna-images/answer/aaf0807f-1331-4604-8d59-0bda73a29e80.jpg

Answered: Arrange the given steps in the correct…

Math

Advanced Math

Arrange the given steps in the correct order to prove that 3" 6, 3k E search e

Advanced Engineering Mathematics

10th Edition

ISBN:9780470458365

Author:Erwin Kreyszig

Publisher:Erwin Kreyszig

Chapter2: Second-order Linear Odes

Section: Chapter Questions

Problem 1RQ

See similar textbooks

Similar questions

Kindly give me a detailed answer in a clear handwriting of all the subparts by mentioning the subpart's name. It is one whole question including the formulas. All the subparts are related. I am attaching the full question. All the questions are related. This is my second time uploading these questions as I got wrong answers previously. So kindly answer this one by following the given instructions. I will upvote if the answer is correct. Thank you. Download the question so that you can read it. I only have few minutes.
A student wants to earn a C for a class. To get this grade, the average of his six test scores must be 70. He has the following grades on five tests: 60, 78, 65, 68, 72 What grade must the student get on the next test so that the average of his scores is 70? Enter your answer as a number, like this: 42
I only need answers to the 3 unanswered questions
Please write the steps of this question and circle the answer so that I can understand. Please write the answer in an organized way if possible so that I can understand and identify the numbers. For each step, please specify which answer corresponds to which step. I appreciate your understanding. This question has several steps and I have sent you both pages. Please, if possible, write the step by step and circle the answer so that I don't get lost. Please tell me what the answer to each question is about.
please could you solve the questions are highlighted with yellow color. please show all work.
I want all solved please thanks for first 3
Find two numbers a and b whose sum a + b is 3 and whose difference a – b is -7. Your answer is a = b = Submit Question hp
Please they are all algebra questions, thanks
I am doing math right now, and I am in the middle of taking a test. I do not want to look up the answer but this test is important to get my grade up. The question is 12x over 45x multiplied by 20 over 6x. Please help me out!!
Mr. Imperfecto teaches another math class. This time he has 23 students take a test, the average score on which is an 87. Mr. Imperfecto realizes he put the wrong grade in for a student. He entered a 35, and the score should have been an 85. To the nearest integer, what is the new class average?