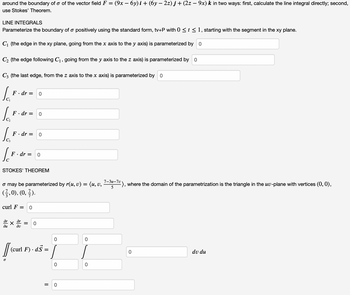
around the boundary of o of the vector field F = (9x − 6y)i + (6y – 2z)j + (2z - 9x) k in two ways: first, calculate the line integral directly; second, use Stokes' Theorem. LINE INTEGRALS Parameterize the boundary of a positively using the standard form, tv+P with 0 ≤ t ≤ 1, starting with the segment in the xy plane. C₁ (the edge in the xy plane, going from the x axis to the y axis) is parameterized by 0 C₂ (the edge following C₁, going from the y axis to the z axis) is parameterized by 0 C3 (the last edge, from the z axis to the x axis) is parameterized by 0 F. dr = 0 lá F. dr = 0 F. dr = 0 C3 1.² 0 F. dr = 0 STOKES' THEOREM o may be parameterized by r(u, v) = (u, v, 7-3u-70), where the domain of the parametrization is the triangle in the uv-plane with vertices (0,0), (7,0), (0,7). 5 curl F = 0 0 (curl F). ds = = 0 J 0 0 0 0 du du

Along the curve C traced out by the end point of the position vector tk (t) = (- sin ti + cos tj+t) = [0,π/2] calculate the line integral √ F(r) - di dr of the vector field F(x, y, z) = −y+xj+yzk.

Let f(x, y) = 7x cos (y). Find the conservative vector field F, which is the gradient of f. (Give your answer using component form or standard basis vectors. Express numbers in exact form. Use symbolic notation and fractions where needed.) F = (7 cos (y).-7x sin(y) Evaluate the line integral of F over the upper half of the unit circle centered at the origin, oriented clockwise. (Give an exact answer. Use symbolic notation and fractions where needed.) C F. dr = Incorrect 12 Question Source: Rogawski 4e Calculus Early Transcendentals Publisher: W.H. Freema 5.02. D

Use Stokes' Theorem to calculate the circulation of the field F around the curve C in the indicated direction 3₁ F = 2yi +5xj + z³k; C: the counterclockwise path around the perimeter of the triangle in the x-y plane formed from the x-axis, y- axis, and the line y = 5 - 6x