
Elementary Geometry For College Students, 7e
7th Edition
ISBN: 9781337614085
Author: Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher: Cengage,
expand_more
expand_more
format_list_bulleted
Question
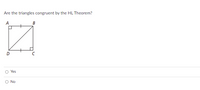
Transcribed Image Text:**Title: Are the triangles congruent by the HL Theorem?**
**Diagram Explanation:**
The diagram shows a square with a diagonal line. The square is labeled with points A, B, C, and D, creating two triangles: triangle ABD and triangle BCD. Both triangles are right triangles due to the 90-degree angles at points A and C. The side AD is congruent to side BC (indicated by hash marks). The diagonal line BD is the hypotenuse shared by both triangles.
**Question:**
Are the triangles congruent by the HL Theorem?
**Options:**
- ○ Yes
- ○ No
**Explanation of HL Theorem:**
The Hypotenuse-Leg (HL) Theorem states that two right triangles are congruent if the hypotenuse and one leg of one right triangle are congruent to the hypotenuse and one leg of another right triangle.
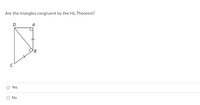
Transcribed Image Text:**Question:**
Are the triangles congruent by the HL Theorem?
**Diagram Explanation:**
The diagram shows two right triangles, ΔDCA and ΔCBA. The triangle ΔDCA shares the side DC with ΔCBA, making it the common hypotenuse for both triangles. Each triangle has one right angle (marked by a square). The leg CA is marked as equal in both triangles.
**Answer Options:**
- ○ Yes
- ○ No
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Similar questions
- Help me pleasearrow_forwardWrite a proof in the format of your choice of the isosceles triangle theorem. Given: AB BC BD is the perpendicular bisector of AC Prove:arrow_forwardWhich two triangles are congruent by the SSS Theorem? Complete the congruence statement. B HHHH CH A A X Y I 344 Z J 0 S 0arrow_forward
Recommended textbooks for you
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning

Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,

Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning