
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
Please help with n=32
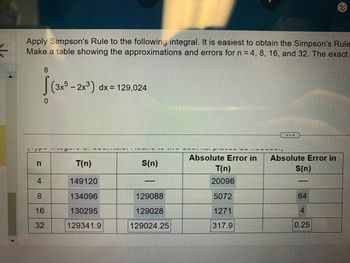
Transcribed Image Text:**Using Simpson's Rule for Numerical Integration**
In this section, we'll apply Simpson's Rule to approximate the integral of the function \( \int_0^8 (3x^5 - 2x^3) \, dx \), with the exact value being 129,024. We'll provide a table showing approximations and errors for different segment values \( n = 4, 8, 16, \) and \( 32 \).
**Table of Approximations and Errors**
| \( n \) | \( T(n) \) | \( S(n) \) | Absolute Error in \( T(n) \) | Absolute Error in \( S(n) \) |
|---------|-----------|----------|-------------------------|-------------------------|
| 4 | 149,120 | — | 20,096 | — |
| 8 | 134,096 | 129,088 | 5,072 | 64 |
| 16 | 130,295 | 129,028 | 1,271 | 4 |
| 32 | 129,341.9 | 129,024.25 | 317.9 | 0.25 |
**Explanation:**
- \( T(n) \) refers to the approximation using the Trapezoidal Rule.
- \( S(n) \) refers to the approximation using Simpson's Rule.
- The absolute errors for each method are calculated by comparing the approximation with the exact integral value \( 129,024 \).
Simpson's Rule generally provides a more accurate approximation, as evidenced by smaller errors compared to the Trapezoidal Rule, particularly as \( n \) increases.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 4 steps

Knowledge Booster
Similar questions
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

