
A First Course in Probability (10th Edition)
10th Edition
ISBN: 9780134753119
Author: Sheldon Ross
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Question
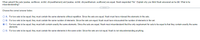
Transcribed Image Text:When asked if the sets {azalea, sunflower, orchid, chrysanthemum} and {azalea, orchid, chrysanthemum, sunflower} are equal, Noah responded "No". Explain why you think Noah answered as he did. What is he
misunderstanding?
Choose the correct answer below.
O A. For two sets to be equal, they must contain the same elements without repetition. Since the sets are equal, Noah must have misread the elements in the sets.
O B. For two sets to be equal, they must contain the same number of elements. Since the sets are equal, Noah must have miscounted the number of elements in the set.
O C. For two sets to be equal, they must both contain exactly the same elements. Since the sets are equal, Noah must misunderstand that the only requirement for sets to be equal is that they contain exactly the same
elements.
O D. For two sets to be equal, they must contain the same elements in the same order. Since the sets are not equal, Noah is not misunderstanding anything.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 1 images

Knowledge Booster
Similar questions
- ges. The results 89 take French. 92 take German. 44 take French and German. 47 take German and Russian. 19 take French as their only foreign language. 23 take French, Russian, and German.arrow_forwarddæ Evaluate V4x – x2 A. 2 3 C. 4 D. A E. NONE OF THE ABOVE B.arrow_forward-7 Let A= -4 -3 Find 5A. 5A = 3.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 A First Course in Probability (10th Edition)ProbabilityISBN:9780134753119Author:Sheldon RossPublisher:PEARSON
A First Course in Probability (10th Edition)ProbabilityISBN:9780134753119Author:Sheldon RossPublisher:PEARSON

A First Course in Probability (10th Edition)
Probability
ISBN:9780134753119
Author:Sheldon Ross
Publisher:PEARSON
