analyze the dipole for dipole moment in azdirection.

Electric Dipole

If two charges of equal magnitude and opposite signs are placed at a very small distance from one another, then the system is known as an electric dipole. The strength of an electric dipole is measured by its dipole moment vector. If the magnitude of the charge is $q$ and the separation between the charges is $2a$ then the dipole moment is given by

$\overrightarrow{p}=q.2a\hat{p}$

The direction of the dipole moment is from the negative to the positive charge.

Let us consider two charges $q$ and $-q$ be placed at a distance of $2a$. Let $\overrightarrow{r}$ be the distance between the center of the dipole and the point of interest $P$. Let $\overrightarrow{r_1}$ and $\overrightarrow{r_2}$ be the distance between the point P and $+q$ and $-q$ respectively. 

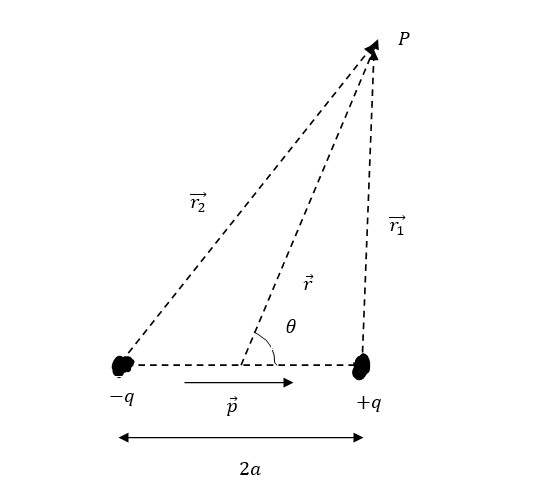
Potential due to charge $-q$ at P$=\frac{1}{4{\mathrm{\pi \epsilon }}_0}\frac{-q}{r_2}$

Potential due to charge $+q$ at P$=\frac{1}{4{\mathrm{\pi \epsilon }}_0}\frac{q}{r_1}$

The total potential at P is

$\begin{array}{rcl}V& =& \frac{1}{4{\mathrm{\pi \epsilon }}_0}\frac{q}{r_1}-\frac{1}{4{\mathrm{\pi \epsilon }}_0}\frac{q}{r_2}\\ & =& \frac{1}{4{\mathrm{\pi \epsilon }}_0}\left(\frac{1}{r_1}-\frac{1}{r_2}\right)\end{array}$

Applying cosine law of vector we have

$$\begin{gathered} r_1^2=r^2+a^2-2ra\cos \theta \\ \Rightarrow r_1={\left(r^2+a^2-2ra\cos \theta \right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.} \\ \Rightarrow r_1=r{\left(1+\frac{a^2}{r^2}-2\frac{a}{r}\cos \theta \right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.} \end{gathered}$$

Now for a short dipole, we have

$$\begin{gathered} r_1=r{\left(1-\frac{2a}{r}\cos \theta \right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.} \\ \Rightarrow \frac{1}{r_1}=\frac{1}{r}{\left(1-\frac{2a}{r}\cos \theta \right)}^{-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.} \\ \Rightarrow \frac{1}{r_1}=\frac{1}{r}\left(1+\frac{a}{r}\cos \theta \right) \end{gathered}$$

Similarly, we can see that

$\frac{1}{r_2}=\frac{1}{r}\left(1-\frac{a}{r}\cos \theta \right)$

Therefore the potential 

$$\begin{gathered} V=\frac{q}{4{\mathrm{\pi \epsilon }}_0}\left[1+\frac{a}{r}\cos \theta -1+\frac{a}{r}\cos \theta \right] \\ =\frac{q\times 2a\cos \theta }{4{\mathrm{\pi \epsilon }}_0{\mathrm{r}}^2}=\frac{1}{4{\mathrm{\pi \epsilon }}_0}\frac{p\cos \theta }{r^2} \\ =\frac{1}{4{\mathrm{\pi \epsilon }}_0}\frac{\overrightarrow{p}.\hat{r}}{r^2} \end{gathered}$$

In the question given, the dipole is located at the position $\hat{i}+\hat{j}$ and the position of the observation point is $5\hat{i}+6\hat{j}$. Therefore

$\overrightarrow{r}=\left(5\hat{i}+6\hat{j}\right)-\left(\hat{i}+\hat{j}\right)=4\hat{i}+5\hat{j}$

Therefore

$r^2=4^2+5^2=16+25=41$

and 

$\hat{r}=\frac{\overrightarrow{r}}{r}=\frac{4}{\sqrt{41}}\hat{i}+\frac{5}{\sqrt{41}}\hat{j}$

Let the dipole moment is given by

$\overrightarrow{p}=p_x\hat{i}+p_y\hat{j}+p_z\hat{k}$

Therefore we have

$9=\frac{1}{4{\mathrm{\pi \epsilon }}_0}\frac{{\displaystyle \frac{4p_x}{\sqrt{41}}}+{\displaystyle \frac{5p_y}{\sqrt{41}}}}{41}$

Thus we wee that there is no component of the dipole moment in the z-direction, that is, $p_z=0$.

Considering the dipole is kept on the x axis. Therefore

$$\begin{gathered} \overrightarrow{r}.\hat{i}=r\cos \theta \\ \Rightarrow \cos \theta =\frac{4}{\sqrt{41}} \end{gathered}$$

Therefore the magnitude of the dipole moment

$$\begin{gathered} 9=\frac{1}{4{\mathrm{\pi \epsilon }}_0}\frac{p{\displaystyle \frac{4}{\sqrt{41}}}}{41} \\ \Rightarrow p=9\times 4\mathrm{\pi }\times 8.85\times {10}^{-12}\times 41\times \frac{\sqrt{41}}{4}\mathrm{Cm}=6.56\times {10}^{-8} \mathrm{Cm} \end{gathered}$$