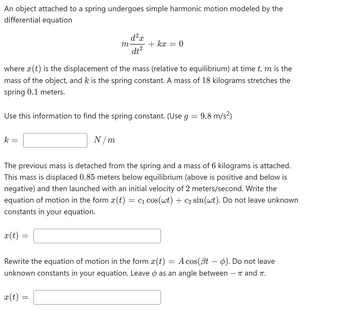
An object attached to a spring undergoes simple harmonic motion modeled by the differential equation = m. N/m x (t) d²x dt² + kx where x(t) is the displacement of the mass (relative to equilibrium) at time t, m is the mass of the object, and k is the spring constant. A mass of 18 kilograms stretches the spring 0.1 meters. Use this information to find the spring constant. (Use g 9.8 m/s²) - 0 The previous mass is detached from the spring and a mass of 6 kilograms is attached. This mass is displaced 0.85 meters below equilibrium (above is positive and below is negative) and then launched with an initial velocity of 2 meters/second. Write the equation of motion in the form x (t) = C₁ cos(wt) + C₂ sin(wt). Do not leave unknown constants in your equation. = Rewrite the equation of motion in the form (t) A cos(Bt - 6). Do not leave unknown constants in your equation. Leave as an angle between - and T. x(t) =

Q: Solve the following initial value problem. y (3) - 2y + y' = 2 + 8xe*; y(0) = y'(0) = 0, y''(0) = 1…

A:

Q: 4. For a satellite to maintain an orbit of h kilometers altitude, its speed (in km/s) must be equal…

A: Given, for a satellite to maintain an orbit of h kilometers altitude, its speed (in km/s) must be…

Q: Consider a linear system whose augmented matrix is For what value of k will the system have no…

A: Consider the Augmented matrix .To Find:For what value of k will the system have no solution?

Q: se the graph of the function f(x) and the table of the invertible function k(x) to answer each…

A:

Q: Given c = -27 + 8j and a = 107 + 4j, find ||ē+ ā|| and |||| + ||ā||. and a = 107 + 43,1 Give EXACT…

A:

Q: pls solve all parts- What is the number ak of solutions? (a) y₁ ++yn = k where 0 ≤ y ≤ m. (b) x₁ +…

A: To find the number  of solutionsa)   where .b)   where c)   where ,  is even and  is odd.

Q: 725 Differentiate function y using logarithmic differentation. (2-92)√√2+1 Hint: use logarithm on…

A:

Q: 1 *² = ² + 1 √/4 + 1/ ²0 V Prove that 4+ ¡dx is a convergent improper integral.

A:

Q: Suppose f: R→→ R is convex. Show that for all x € [a, b]. x-a :) ≤ b = = f(a) + ² = f(b) b a f(x) ≤

A: Suppose   is convex. We have to show that:

Q: a. Find the general flow pattern of the network shown in the figure. b. Assuming that the flow must…

A:

Q: Solve step by step in digital format Solve for Ricatti dy dx = -2-y + y² answer y =,2 + 1 ce-3x_…

A:

Q: Evaluate the integral. 7 I'v x² + 49 dx

A:

Q: 2/y²+4) Dx + (1-x²)ydy=0

A:

Q: 4. Consider the following autonomous first-order differential equation. dy = y² (y²-9). dx Find the…

A: For an autonomous system of the form: , it can be written that:The region above or below the…

Q: Solve for the following problem and show your complete solutions. A 10ft long horizontal trough has…

A: Geometry of the TroughThe trough has ends shaped like equilateral triangles with sides of 6 ft. The…

Q: 9. Prove that n - n is divisible by 30 for every integer n. te

A:

Q: 7. Prove that n, n +4, n +8 are all primes if and only if n = 3.

A:

Q: 5. A recent college graduate has job offers for a sales position at two computer companies. Job A…

A: Job A pays: $50,000 per year plus 10% commission.Job B pays: $40,000 per year plus 20%…

Q: Show that the set is infinite by placing it in a one-to-one correspondence with a proper subset of…

A:

Q: The matrix A= -4 -4 8 2 2 -4 has two real eigenvalues, one of multiplicity 1 and one of multiplicity…

A: Given:The given matrix is .To Find:We have to determine the eigenvalues and the basis of each…

Q: Apply Newton's Method to approximate the x-value(s) of the indicated point(s) of intersection of the…

A: We have plotted the graphs of f(x)=x and g(x)=tan⁡x in the following graph.Since the required…

Q: Problem 1.16 Sketch the vector function multiplies T. nary vector in ↑ r.2 and compute its…

A:

Q: Consider A = -2 10 -13] -2 4 -1 -1 -1 1 If the Gram-Schmidt process is applied to determine the QR…

A:

Q: Define for n ≥ 1, fn(x) = limn→∞ ₁ fn (x) dx = 0 because fn (x)0 uniformly. True 1 nx² +1' False…

A:

Q: Breadco Bakeries is a new bakery chain that sells bread to customers throughout the state of…

A:

Q: Texas is planning to build a high-speed commuter rail system to connect major cities in the state.…

A: Given the distance between the cities in the table below,AustinCorpusDallasFort WorthHoustonSan…

Q: 8. Let n ≥ 2. Prove that (n+1)! + k is composite for k = 2,..., n + 1. This shows that there exist…

A:

Q: Find all x in R4 that are mapped into the zero vector by the transformation x→Ax for the given…

A:

Q: 2. The Fibonacci numbers F(0), F(1), F(2),… are defined as follows: F(0) := 0 F(1) := 1 F(n) := F(n…

A:

Q: 11. The prime numbers p and q are called twin primes if |pq|= 2. Let p and q be primes. Prove that…

A: and are primr number and they are said to be twine prime if We have to show  is a square if and only…

Q: Find the orthogonal projection of v = projy(v) = 61 29 4 3 onto the subspace V of R3 spanned by -4…

A:

Q: 7. 4y"+y= 2 sec (1/2), -π < t < T

A:

Q: Describe all solutions of Ax = 0 in parametric vector form, where A is row equivalent to the given…

A:

Q: an n→∞ An + 1 2 = 0. Show that lim an n→∞ (5) Suppose lim = 2.

A:

Q: Consider an economy with three sectors, Chemicals & Metals, Fuels & Power, and Machinery. Chemicals…

A: Given:It is given that there is an economy with three sectors,Chemicals and MetalsFuels and…

Q: Consider the following graph. V(G) = (v1, v2, v3, v4}, e(G) = {e1,e2, e3, e4, e5}, E(G) = {(e1, [v1,…

A: Given data is

Q: Solve step by step in digital format Solve the exact differential equation (2x + 4) dx + (3y - 1) dy…

A: A differential equation of the form  is said to be exact if the left hand member is the exact…

Q: Recall Ackermann's function: 2n 0 2 A(m 1, A(m, n − 1)) Prove that A(1, n) = 2" for n ≥ 1 by using…

A: Given the Ackermann's function We need to prove that  for  by using the mathematical induction.

Q: Determine if v is in the set spanned by the columns of B. B= 3-3 2 9 7 8 9 3 14 6 -2 12 V = - 11 21…

A:

Q: Suppose that at the end of each week for 30 years, $200 is deposited into an account that earns 5.9%…

A:

Q: a) Use the Euler formula, e¹⁰ (cos(0) + i sin(0))" = cos(n) + i sin(n). b) Suppose y(t) = e-2t eit…

A: In this question, we will find the solution to the given problem.

Q: 1. Let G be a group. For any g E G and n = Z, we define if n > 0; g" = 99, n g • 9 |n| 9 if n = 0;…

A:

Q: Workers in the U.S. pay several types of taxes on income. The lesson discussed the FICA taxes. You…

A: (a) The  tax rate everyone pays on the first $8,500 of income:From the given tax table: the first…

Q: Let A = 4n +3 { : n = NU N}U (0,¹]. Fir Find 5n-1

A:

Q: Prove That The magnitude of The Vector does not change by turning when you ще The array CSO Sino…

A: To show that the magnitude of a vector does not change when we use the array  to rotate the vector…

Q: Use the image above to identify and explain the relationship between the segments and circles A and…

A: Given Information:The diagram with circles and lines are provided.Objective:Write the relationship…

Q: Determine the value of c that would make the points fit an exponential relationship with base 0.25.…

A:

Q: For the next 3 problems - Find the equation of the line graphed, find a second equation so that the…

A: The graph of the first equation y=−x+6 is givenWe need to find a second equation such that it has…

Q: Design a signature σvs suitable for ℚ-vector spaces (i.e. vector spaces over ℚ) and define its…

A:

Q: Find the genera solution of the given differential equation. dy x + 3y = x³ - x dx y(x) = Give the…

A: