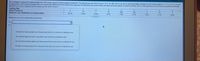
I need the bull & alternative hypotheses, test statistic, critical value , & conclusion Thankyou so much An investigator analyzed the leading digits from 784 checks issued by seven suspect companies. The frequencies were found to be 2, 15, 0, 73, 495, 163, 9, 22, and 5, and those digits correspond to the leading digits of 1, 2, 3, 4, 5, 6, 7, 8, and9, respectively. If the observed frequencies are substantially different from the frequencies expected with Benford's law shown below, the check amounts appear to result from fraud. Use a 0.025 significance level to test for goodness-of-fit withBenford's law. Does it appear that the checks are the result of fraud?Leading DigitActual FrequencyBenford's Law: Distribution of Leading Digits4739.7%31517.6%61636.7%495225.1%30.1%12.5%5.7.9%5.8%4.6%Determine the null and alternative hypotheses.HoH,:At least two leading digits have frequencies that do not conform to Benford's law.The leading digits are from a population that conforms to Benford's law.At most three leading digits have frequencies that do not conform to Benford's law.At least one leading digit has a frequency that does not conform to Benford's law. 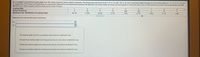An investigator analyzed the leading digits from 784 checks issued by seven suspect companies. The frequencies were found to be 2, 15, 0, 73, 495, 163, 9, 22, and 5, and those digits correspond to the leading digits of 1, 2, 3, 4, 5, 6, 7, 8, and9, respectively. If the observed frequencies are substantially different from the frequencies expected with Benford's law shown below, the check amounts appear to result from fraud. Use a 0.025 significance level to test for goodness-of-fit withBenford's law. Does it appear that the checks are the result of fraud?Leading DigitActual FrequencyBenford's Law: Distribution of Leading Digits163230.1%15739.7%95.8%225.1%49517.6%12.5%7.9%6.7%4.6%Determine the null and alternative hypotheses.HoH,:The leading digits are from a population that conforms to Benford's law.At most three leading digits have frequencies that do not conform to Benford's law.At least two leading digits have frequencies that do not conform to Benford's law.At least one leading digit has a frequency that does not conformBenford's law.

There is only one categorical variable which is leading digit. It has 9 categories. We have to do test whether the observed frequencies are substantially different from the frequencies expected with Bedford’s law or not. Since there is only one categorical variable, this is Chi-Square test for goodness-of-fit.The null and alternative hypotheses are H0: The leading digits are from a population that confirms to Bonford’s law. H1: At least one leading digit has a frequency that does not confirm to Bonford’s law.Leading digit observed expected O - E (O - E)² / E 1 2 784 (0.301) = 235.984 -233.984 232.001 2 15 784 (0.176) = 137.984 -122.984 109.615 3 0 784 (0.12) = 98.000 -98.000 98.000 4 73 784 (0.097) = 76.048 -3.048 0.122 5 495 784 (0.079) = 61.936 433.064 3028.036 6 163 784 (0.067) = 52.528 110.472 232.334 7 9 784 (0.058) = 45.472 -36.472 29.253 8 22 784 (0.051) = 39.984 -17.984 8.089 9 5 784 (0.046) = 36.064 -31.064 26.757 Total 784 784.000 0.000 3764.207 The value of the test statistic is χ2= 3764.207.Df = n-1 = 9-1 = 8 EXCEL command is “= CHIDIST (x, deg_freedom)” For p-value, enter in EXCEL as, “= CHIDIST (3764.207, 8)” P-value = 0.0000. Conclusion: Since p-value (=0.0000) ≤(=0.025), then reject the null hypothesis. There is sufficient evidence to conclude that at least one leading digit has a frequency that does not confirm to Bedford’s law.