
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
Please help me with these questions. I am ha understanding what
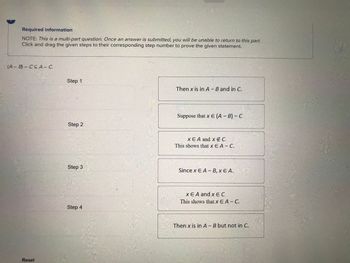
Transcribed Image Text:Required information
NOTE: This is a multi-part question. Once an answer is submitted, you will be unable to return to this part.
Click and drag the given steps to their corresponding step number to prove the given statement.
(A-B) CCA- C.
Reset
Step 1
Step 2
Step 3
Step 4
Then x is in A - B and in C.
Suppose that x E (A - B) - C
x EA and x E C.
This shows that x EA - C.
Since x EA-B, XEA.
XEA and x E C.
This shows that Xx EA - C.
Then x is in A - B but not in C.
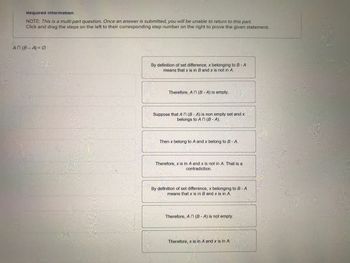
Transcribed Image Text:Required information
NOTE: This is a multi-part question. Once an answer is submitted, you will be unable to return to this part.
Click and drag the steps on the left to their corresponding step number on the right to prove the given statement.
An (B-A) = 0
By definition of set difference, x belonging to B-A
means that x is in B and x is not in A.
Therefore, An (B-A) is empty.
Suppose that An (B-A) is non empty set and x
belongs to An (B-A).
Then x belong to A and x belong to B - A.
Therefore, x is in A and x is not in A. That is a
contradiction.
By definition of set difference, x belonging to B-A
means that x is in B and x is in A.
Therefore, An (B-A) is not empty.
Therefore, x is in A and x is in A.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 3 steps with 4 images

Knowledge Booster
Similar questions
- Can you explain the second question/step 2 more clearly? I'm having trouble following what to do.arrow_forwardI'm still not understanding the answer to this specific question please clarify furtherarrow_forwardhello, I appreciate your answer but the answer looks funny it is difficult to understand. Would you please rewrite the answer in a way I can understand? Thank you.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

