Age Group 15-24 25-34 35-44 45-64 years years years years 6. 4 Male 3. Female 3. 3 4 6. Sex
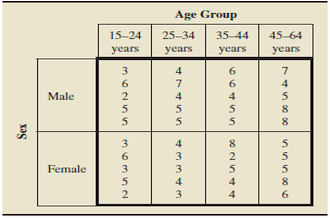
Hospital Stays. The U.S. National Center for Health Statistics collects data on length of stay in noninstitutional, short-stay hospitals by sex and age. Results are published in Vital and Health Statistics. Independent random samples of Americans were taken to compare the lengths of stay (in days) for males and females in four age groups (15–24 years, 25–34 years, 35–44 years, and 45–64 years). The data are in the following table.
a. the response variable
b. the factors
c. the levels of each factor
d. the number of treatment combinations
e. the experimental units
f. the number of observations for each treatment combination
g. the experimental factors, if any
h. the classification factors, if any
i. whether the study is a designed experiment or an observational study
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 3 images
