
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
Using basic

Transcribed Image Text:The chalkboard contains mathematical expressions related to sequences and their limits in the real numbers (denoted as \( \mathbb{R} \)).
1. **Sequences Definitions and Limits:**
- \( X = (x_n) \) in \( \mathbb{R}^p \)
- \( Y = (y_n) \) in \( \mathbb{R}^p \)
These describe sequences \( X \) and \( Y \), with terms \( x_n \) and \( y_n \), respectively, each existing in a p-dimensional real space.
2. **Convergence of Sequences:**
- \( x_n \to x \in \mathbb{R} \)
- \( y_n \to y \in \mathbb{R} \)
This indicates that the sequences \( x_n \) and \( y_n \) converge to the limits \( x \) and \( y \), both of which are real numbers.
3. **Combined Limit Expression:**
- \( X \cdot Y = (x_n \cdot y_n) \)
- It is stated that \( x_n \cdot y_n \to x \cdot y \) as \( n \) approaches infinity.
4. **Inequality and Result to Show:**
- Show \( |x_n y_n - x y| < \epsilon \)
The task is to demonstrate that the absolute difference between the product of terms from the sequences and the product of their limits is less than a given small positive value \( \epsilon \).
The expressions and tasks are typical for studies on the behavior of sequences and their limits, often encountered in real analysis or advanced calculus courses. There's no graph or diagram; the focus is on the algebraic manipulation of limits and understanding convergence.
Expert Solution
arrow_forward
Step 1
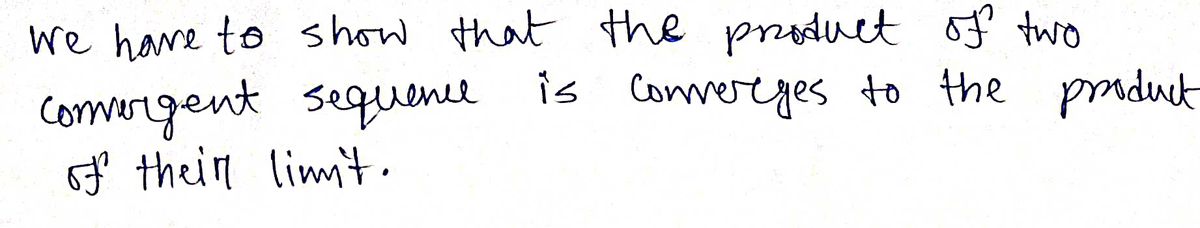
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps with 3 images

Knowledge Booster
Similar questions
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

