5.6 INHOMOGENEOUS BOUNDARY CONDITIONS In this section we consider problems with sources given at the boundary. We shall see that naive use of the separation of variables technique will not work. Let's begin with the diffusion equation with sources at both endpoints. u₁ = kuxx u(0,t)=h(t) 00 u(l,t) = j(t) u (x, 0) = 0. A separated solution u = X(x)T(t) just will not fit the boundary conditions. So we try a slightly different approach. EXPANSION METHOD We already know that for the corresponding homogeneous problem the correct expansion is the Fourier sine series. For each t, we certainly can expand u(x,t) = Σun(t) sin - n=1 2 -76- un(t) = 0=ut - kuxx = for some coefficients un(t), because the completeness theorems guarantee that any function in (0, 1) can be so expanded. The coefficients are necessarily given by nTX 1 Σ[ илх u(x, t) sin dx. 1 (3) You may object that each term in the series vanishes at both endpoints and thereby violates the boundary conditions. The answer is that we simply do not insist that the series converge at the endpoints but only inside the interval. In fact, we are exactly in the situation of Theorems 3 and 4 but not of Theorem 2 of Section 5.4. Now differentiating the series (2) term by term, we get dun dt (1) +kun (1) (7) ²] sin (2) плх So the PDE seems to require that dun/dt + kλnun = 0, so that un(t) = Anet. There is no way for this to fit the boundary conditions. Our method fails! What's the moral? It is that you can't differentiate term by term. See Example 3 in Section 5.4 for the dangers of differentiation. Let's start over again but avoid direct differentiation of the Fourier series. The expansion (2) with the coefficients (3) must be valid, by the completeness theorem 5.4.3, say, provided that u(x, t) is a continuous function. Clearly, the initial condition requires that u,,(0) = 0. If the derivatives of u(x, t) are also continuous, let's expand them, too. Thus with V₁ (1) = du at with the coefficients 2 a²u əx² dx2 = Wn(t)= u(x, t) sin n=1 vn (1) - kwn (1) = V₁ (1) sin ди ηπε sin at T The last equality is valid since we can differentiate under an integral sign if the new integrand is continuous (see Section A.3). We also expand илх 1 n=1 2 a²u =75% əx² By Green's second identity (5.3.3) the last expression equals 2 + ²7 (ux ηπ.Χ 1 Wn(1) sin dx = dx + sin плх 1 dun dt NAX =76 So from (5) and (8) we deduce that u, (1) satisfies е dx. 7(77)²(x,1 Here come the boundary conditions. The sine factor vanishes at both ends. The last term will involve the boundary conditions. Thus w₁(t)=-λun(t)-2nal-2(-1)" j(t) + 2xl-²h(t), where λ = (n/1). Now by (5) and (7) the PDE requires η π.χ ux sin пл nлx Tucos T (u₁-kux) sindx = -fo=o. 0=0. (4) dun = k{-λnun(1) - 2nлl-²[(-1)" j(t)-h(t)]}. dt (5) (6) (7) 1 (8) (9) This is just an ordinary differential equation, to be solved together with the initial condition u,(0) = 0 from (1). The solution of (9) is Un(t) = Ce-akt - 2n71-²ks e-hak(-s)[(-1)" j(s)- h(s)] ds. (10) As a second case, let's solve the inhomogeneous wave problem un-c²uxx = f(x, t) u(0,t)=h(t) u(x, 0) = p(x) and, just as before, Again we expand everything in the eigenfunctions of the corresponding ho- mogeneous problem: Therefore, u(x, t) = [u,(t) sin n=1 u₁(x, t) with coefficients un(t), uxx(x, t) with coefficients wn(t), f(x, t) with coefficients fn(t), p(x) with coefficients on, and (x) with coefficients Vn. Then u(l,t)=k(t) u,(x, 0) = (x). Wn (1) = 2 2²u ηπχ Un (1) == sin dx = at² 1 =76 From the PDE we also have Un(1) - C²w₁(1) = ²√ √ ² 2 a²u η π.χ sin ax² = -λnun (1) +2nлl-²[h(t)-(-1)"k(t)]. d²un d1² with the initial conditions илх I - dx d²un d1² (un-c²uxx) sin dx = fn(t). ηπχ 1 (11) +c²λnun(t) = -2nлl-² [(-1)"k(t)-h(t)] + fn(t) un (0) = Φη u' (0) = Vn. The solution can be written explicitly (see Exercise 11). (12) 1. 2. find u (x, t) for 0 < x < 1 and t> 0 which solves UtUxx = 0, u (x,0) = 1, ux (1,t) = t, find u (x, t) for 0 < x < 1 and t > 0 which solves Ut - Uxx = et, u (x,0) = 1, ux (0, t) = 0. u (1, t) = u (0,t) = 0.
5.6 INHOMOGENEOUS BOUNDARY CONDITIONS In this section we consider problems with sources given at the boundary. We shall see that naive use of the separation of variables technique will not work. Let's begin with the diffusion equation with sources at both endpoints. u₁ = kuxx u(0,t)=h(t) 00 u(l,t) = j(t) u (x, 0) = 0. A separated solution u = X(x)T(t) just will not fit the boundary conditions. So we try a slightly different approach. EXPANSION METHOD We already know that for the corresponding homogeneous problem the correct expansion is the Fourier sine series. For each t, we certainly can expand u(x,t) = Σun(t) sin - n=1 2 -76- un(t) = 0=ut - kuxx = for some coefficients un(t), because the completeness theorems guarantee that any function in (0, 1) can be so expanded. The coefficients are necessarily given by nTX 1 Σ[ илх u(x, t) sin dx. 1 (3) You may object that each term in the series vanishes at both endpoints and thereby violates the boundary conditions. The answer is that we simply do not insist that the series converge at the endpoints but only inside the interval. In fact, we are exactly in the situation of Theorems 3 and 4 but not of Theorem 2 of Section 5.4. Now differentiating the series (2) term by term, we get dun dt (1) +kun (1) (7) ²] sin (2) плх So the PDE seems to require that dun/dt + kλnun = 0, so that un(t) = Anet. There is no way for this to fit the boundary conditions. Our method fails! What's the moral? It is that you can't differentiate term by term. See Example 3 in Section 5.4 for the dangers of differentiation. Let's start over again but avoid direct differentiation of the Fourier series. The expansion (2) with the coefficients (3) must be valid, by the completeness theorem 5.4.3, say, provided that u(x, t) is a continuous function. Clearly, the initial condition requires that u,,(0) = 0. If the derivatives of u(x, t) are also continuous, let's expand them, too. Thus with V₁ (1) = du at with the coefficients 2 a²u əx² dx2 = Wn(t)= u(x, t) sin n=1 vn (1) - kwn (1) = V₁ (1) sin ди ηπε sin at T The last equality is valid since we can differentiate under an integral sign if the new integrand is continuous (see Section A.3). We also expand илх 1 n=1 2 a²u =75% əx² By Green's second identity (5.3.3) the last expression equals 2 + ²7 (ux ηπ.Χ 1 Wn(1) sin dx = dx + sin плх 1 dun dt NAX =76 So from (5) and (8) we deduce that u, (1) satisfies е dx. 7(77)²(x,1 Here come the boundary conditions. The sine factor vanishes at both ends. The last term will involve the boundary conditions. Thus w₁(t)=-λun(t)-2nal-2(-1)" j(t) + 2xl-²h(t), where λ = (n/1). Now by (5) and (7) the PDE requires η π.χ ux sin пл nлx Tucos T (u₁-kux) sindx = -fo=o. 0=0. (4) dun = k{-λnun(1) - 2nлl-²[(-1)" j(t)-h(t)]}. dt (5) (6) (7) 1 (8) (9) This is just an ordinary differential equation, to be solved together with the initial condition u,(0) = 0 from (1). The solution of (9) is Un(t) = Ce-akt - 2n71-²ks e-hak(-s)[(-1)" j(s)- h(s)] ds. (10) As a second case, let's solve the inhomogeneous wave problem un-c²uxx = f(x, t) u(0,t)=h(t) u(x, 0) = p(x) and, just as before, Again we expand everything in the eigenfunctions of the corresponding ho- mogeneous problem: Therefore, u(x, t) = [u,(t) sin n=1 u₁(x, t) with coefficients un(t), uxx(x, t) with coefficients wn(t), f(x, t) with coefficients fn(t), p(x) with coefficients on, and (x) with coefficients Vn. Then u(l,t)=k(t) u,(x, 0) = (x). Wn (1) = 2 2²u ηπχ Un (1) == sin dx = at² 1 =76 From the PDE we also have Un(1) - C²w₁(1) = ²√ √ ² 2 a²u η π.χ sin ax² = -λnun (1) +2nлl-²[h(t)-(-1)"k(t)]. d²un d1² with the initial conditions илх I - dx d²un d1² (un-c²uxx) sin dx = fn(t). ηπχ 1 (11) +c²λnun(t) = -2nлl-² [(-1)"k(t)-h(t)] + fn(t) un (0) = Φη u' (0) = Vn. The solution can be written explicitly (see Exercise 11). (12) 1. 2. find u (x, t) for 0 < x < 1 and t> 0 which solves UtUxx = 0, u (x,0) = 1, ux (1,t) = t, find u (x, t) for 0 < x < 1 and t > 0 which solves Ut - Uxx = et, u (x,0) = 1, ux (0, t) = 0. u (1, t) = u (0,t) = 0.
Oh no! Our experts couldn't answer your question.
Don't worry! We won't leave you hanging. Plus, we're giving you back one question for the inconvenience.
Submit your question and receive a step-by-step explanation from our experts in as fast as 30 minutes.
You have no more questions left.
Message from our expert:
Our experts are unable to provide you with a solution at this time. Try rewording your question, and make sure to submit one question at a time. We've credited a question to your account.
Your Question:
[Second Order Equations] How do you solve 2? The second picture is for context
![5.6 INHOMOGENEOUS BOUNDARY CONDITIONS
In this section we consider problems with sources given at the boundary. We
shall see that naive use of the separation of variables technique will not work.
Let's begin with the diffusion equation with sources at both endpoints.
u₁ = kuxx
u(0,t)=h(t)
0<x<l, t>0
u(l,t) = j(t)
u (x, 0) = 0.
A separated solution u = X(x)T(t) just will not fit the boundary conditions.
So we try a slightly different approach.
EXPANSION METHOD
We already know that for the corresponding homogeneous problem the correct
expansion is the Fourier sine series. For each t, we certainly can expand
u(x,t) = Σun(t) sin -
n=1
2
-76-
un(t) =
0=ut - kuxx =
for some coefficients un(t), because the completeness theorems guarantee
that any function in (0, 1) can be so expanded. The coefficients are necessarily
given by
nTX
1
Σ[
илх
u(x, t) sin dx.
1
(3)
You may object that each term in the series vanishes at both endpoints and
thereby violates the boundary conditions. The answer is that we simply do not
insist that the series converge at the endpoints but only inside the interval. In
fact, we are exactly in the situation of Theorems 3 and 4 but not of Theorem
2 of Section 5.4.
Now differentiating the series (2) term by term, we get
dun
dt
(1)
+kun (1)
(7) ²] sin
(2)
плх
So the PDE seems to require that dun/dt + kλnun = 0, so that un(t) =
Anet. There is no way for this to fit the boundary conditions. Our method
fails! What's the moral? It is that you can't differentiate term by term. See
Example 3 in Section 5.4 for the dangers of differentiation.
Let's start over again but avoid direct differentiation of the Fourier series.
The expansion (2) with the coefficients (3) must be valid, by the completeness
theorem 5.4.3, say, provided that u(x, t) is a continuous function. Clearly, the
initial condition requires that u,,(0) = 0. If the derivatives of u(x, t) are also
continuous, let's expand them, too. Thus
with
V₁ (1) =
du
at
with the coefficients
2
a²u
əx²
dx2 =
Wn(t)=
u(x, t) sin
n=1
vn (1) - kwn (1) =
V₁ (1) sin
ди ηπε
sin
at T
The last equality is valid since we can differentiate under an integral sign if
the new integrand is continuous (see Section A.3). We also expand
илх
1
n=1
2 a²u
=75%
əx²
By Green's second identity (5.3.3) the last expression equals
2
+ ²7 (ux
ηπ.Χ
1
Wn(1) sin
dx =
dx +
sin
плх
1
dun
dt
NAX
=76
So from (5) and (8) we deduce that u, (1) satisfies
е
dx.
7(77)²(x,1
Here come the boundary conditions. The sine factor vanishes at both ends.
The last term will involve the boundary conditions. Thus
w₁(t)=-λun(t)-2nal-2(-1)" j(t) + 2xl-²h(t),
where λ = (n/1). Now by (5) and (7) the PDE requires
η π.χ
ux sin
пл
nлx
Tucos T
(u₁-kux) sindx =
-fo=o.
0=0.
(4)
dun
= k{-λnun(1) - 2nлl-²[(-1)" j(t)-h(t)]}.
dt
(5)
(6)
(7)
1
(8)
(9)
This is just an ordinary differential equation, to be solved together with the
initial condition u,(0) = 0 from (1). The solution of (9) is
Un(t) = Ce-akt - 2n71-²ks e-hak(-s)[(-1)" j(s)- h(s)] ds. (10)
As a second case, let's solve the inhomogeneous wave problem
un-c²uxx = f(x, t)
u(0,t)=h(t)
u(x, 0) = p(x)
and, just as before,
Again we expand everything in the eigenfunctions of the corresponding ho-
mogeneous problem:
Therefore,
u(x, t) = [u,(t) sin
n=1
u₁(x, t) with coefficients un(t), uxx(x, t) with coefficients wn(t), f(x, t) with
coefficients fn(t), p(x) with coefficients on, and (x) with coefficients Vn.
Then
u(l,t)=k(t)
u,(x, 0) = (x).
Wn (1) =
2 2²u ηπχ
Un (1) ==
sin dx =
at² 1
=76
From the PDE we also have
Un(1) - C²w₁(1) = ²√ √ ²
2 a²u η π.χ
sin
ax²
= -λnun (1) +2nлl-²[h(t)-(-1)"k(t)].
d²un
d1²
with the initial conditions
илх
I
- dx
d²un
d1²
(un-c²uxx) sin dx = fn(t).
ηπχ
1
(11)
+c²λnun(t) = -2nлl-² [(-1)"k(t)-h(t)] + fn(t)
un (0) = Φη u' (0) = Vn.
The solution can be written explicitly (see Exercise 11).
(12)](https://content.bartleby.com/qna-images/question/7c4bfc92-ad55-477d-ac4d-39185defff1d/03f92d11-2305-4ccd-a8db-bbfdc08cd7c2/wc2pi8_thumbnail.jpeg)
Transcribed Image Text:5.6 INHOMOGENEOUS BOUNDARY CONDITIONS
In this section we consider problems with sources given at the boundary. We
shall see that naive use of the separation of variables technique will not work.
Let's begin with the diffusion equation with sources at both endpoints.
u₁ = kuxx
u(0,t)=h(t)
0<x<l, t>0
u(l,t) = j(t)
u (x, 0) = 0.
A separated solution u = X(x)T(t) just will not fit the boundary conditions.
So we try a slightly different approach.
EXPANSION METHOD
We already know that for the corresponding homogeneous problem the correct
expansion is the Fourier sine series. For each t, we certainly can expand
u(x,t) = Σun(t) sin -
n=1
2
-76-
un(t) =
0=ut - kuxx =
for some coefficients un(t), because the completeness theorems guarantee
that any function in (0, 1) can be so expanded. The coefficients are necessarily
given by
nTX
1
Σ[
илх
u(x, t) sin dx.
1
(3)
You may object that each term in the series vanishes at both endpoints and
thereby violates the boundary conditions. The answer is that we simply do not
insist that the series converge at the endpoints but only inside the interval. In
fact, we are exactly in the situation of Theorems 3 and 4 but not of Theorem
2 of Section 5.4.
Now differentiating the series (2) term by term, we get
dun
dt
(1)
+kun (1)
(7) ²] sin
(2)
плх
So the PDE seems to require that dun/dt + kλnun = 0, so that un(t) =
Anet. There is no way for this to fit the boundary conditions. Our method
fails! What's the moral? It is that you can't differentiate term by term. See
Example 3 in Section 5.4 for the dangers of differentiation.
Let's start over again but avoid direct differentiation of the Fourier series.
The expansion (2) with the coefficients (3) must be valid, by the completeness
theorem 5.4.3, say, provided that u(x, t) is a continuous function. Clearly, the
initial condition requires that u,,(0) = 0. If the derivatives of u(x, t) are also
continuous, let's expand them, too. Thus
with
V₁ (1) =
du
at
with the coefficients
2
a²u
əx²
dx2 =
Wn(t)=
u(x, t) sin
n=1
vn (1) - kwn (1) =
V₁ (1) sin
ди ηπε
sin
at T
The last equality is valid since we can differentiate under an integral sign if
the new integrand is continuous (see Section A.3). We also expand
илх
1
n=1
2 a²u
=75%
əx²
By Green's second identity (5.3.3) the last expression equals
2
+ ²7 (ux
ηπ.Χ
1
Wn(1) sin
dx =
dx +
sin
плх
1
dun
dt
NAX
=76
So from (5) and (8) we deduce that u, (1) satisfies
е
dx.
7(77)²(x,1
Here come the boundary conditions. The sine factor vanishes at both ends.
The last term will involve the boundary conditions. Thus
w₁(t)=-λun(t)-2nal-2(-1)" j(t) + 2xl-²h(t),
where λ = (n/1). Now by (5) and (7) the PDE requires
η π.χ
ux sin
пл
nлx
Tucos T
(u₁-kux) sindx =
-fo=o.
0=0.
(4)
dun
= k{-λnun(1) - 2nлl-²[(-1)" j(t)-h(t)]}.
dt
(5)
(6)
(7)
1
(8)
(9)
This is just an ordinary differential equation, to be solved together with the
initial condition u,(0) = 0 from (1). The solution of (9) is
Un(t) = Ce-akt - 2n71-²ks e-hak(-s)[(-1)" j(s)- h(s)] ds. (10)
As a second case, let's solve the inhomogeneous wave problem
un-c²uxx = f(x, t)
u(0,t)=h(t)
u(x, 0) = p(x)
and, just as before,
Again we expand everything in the eigenfunctions of the corresponding ho-
mogeneous problem:
Therefore,
u(x, t) = [u,(t) sin
n=1
u₁(x, t) with coefficients un(t), uxx(x, t) with coefficients wn(t), f(x, t) with
coefficients fn(t), p(x) with coefficients on, and (x) with coefficients Vn.
Then
u(l,t)=k(t)
u,(x, 0) = (x).
Wn (1) =
2 2²u ηπχ
Un (1) ==
sin dx =
at² 1
=76
From the PDE we also have
Un(1) - C²w₁(1) = ²√ √ ²
2 a²u η π.χ
sin
ax²
= -λnun (1) +2nлl-²[h(t)-(-1)"k(t)].
d²un
d1²
with the initial conditions
илх
I
- dx
d²un
d1²
(un-c²uxx) sin dx = fn(t).
ηπχ
1
(11)
+c²λnun(t) = -2nлl-² [(-1)"k(t)-h(t)] + fn(t)
un (0) = Φη u' (0) = Vn.
The solution can be written explicitly (see Exercise 11).
(12)
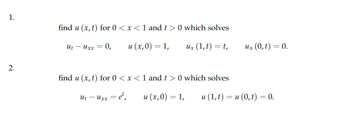
Transcribed Image Text:1.
2.
find u (x, t) for 0 < x < 1 and t> 0 which solves
UtUxx = 0,
u (x,0) = 1,
ux (1,t) = t,
find u (x, t) for 0 < x < 1 and t > 0 which solves
Ut - Uxx = et,
u (x,0) = 1,
ux (0, t) = 0.
u (1, t) = u (0,t) = 0.
Recommended textbooks for you

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

Algebra: Structure And Method, Book 1
Algebra
ISBN:
9780395977224
Author:
Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:
McDougal Littell

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

Algebra: Structure And Method, Book 1
Algebra
ISBN:
9780395977224
Author:
Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:
McDougal Littell
