According to a study done by Nick Wilson of Otago University Wellington, the probability a randomly selected individual will not cover his or her mouth when sneezing is 0.267. Suppose you sit on a bench in a mall and observe people's habits as they sneeze. Complete parts (a) through (c). (a) What is the probability that among 18 randomly observed individuals, exactly 5 do not cover their mouth when sneezing? Using the binomial distribution, the probability is (Round to four decimal places as needed.)
According to a study done by Nick Wilson of Otago University Wellington, the probability a randomly selected individual will not cover his or her mouth when sneezing is 0.267. Suppose you sit on a bench in a mall and observe people's habits as they sneeze. Complete parts (a) through (c). (a) What is the probability that among 18 randomly observed individuals, exactly 5 do not cover their mouth when sneezing? Using the binomial distribution, the probability is (Round to four decimal places as needed.)
Chapter8: Sequences, Series,and Probability
Section8.7: Probability
Problem 4ECP: Show that the probability of drawing a club at random from a standard deck of 52 playing cards is...
Related questions
Question

Transcribed Image Text:According to a study done by Nick Wilson of Otago University Wellington, the probability a randomly
selected individual will not cover his or her mouth when sneezing is 0.267. Suppose you sit on a bench in a
mall and observe people's habits as they sneeze. Complete parts (a) through (c).
(a) What is the probability that among 18 randomly observed individuals, exactly 5 do not cover their mouth
when sneezing?
Using the binomial distribution, the probability is
(Round to four decimal places as needed.)
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 7 images

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
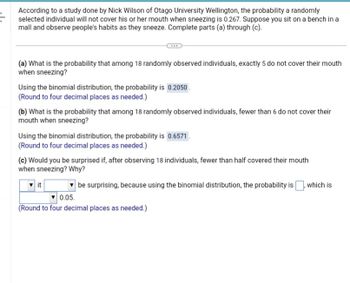
Transcribed Image Text:According to a study done by Nick Wilson of Otago University Wellington, the probability a randomly
selected individual will not cover his or her mouth when sneezing is 0.267. Suppose you sit on a bench in a
mall and observe people's habits as they sneeze. Complete parts (a) through (c).
(a) What is the probability that among 18 randomly observed individuals, exactly 5 do not cover their mouth
when sneezing?
Using the binomial distribution, the probability is 0.2050.
(Round to four decimal places as needed.)
(b) What is the probability that among 18 randomly observed individuals, fewer than 6 do not cover their
mouth when sneezing?
Using the binomial distribution, the probability is 0.6571.
(Round to four decimal places as needed.)
(c) Would you be surprised if, after observing 18 individuals, fewer than half covered their mouth
when sneezing? Why?
be surprising, because using the binomial distribution, the probability is which is
it
0.05.
(Round to four decimal places as needed.)
Solution
Follow-up Question

Transcribed Image Text:According to a study done by Nick Wilson of Otago University Wellington, the probability a randomly
selected individual will not cover his or her mouth when sneezing is 0.267. Suppose you sit on a bench in a
mall and observe people's habits as they sneeze. Complete parts (a) through (c).
(a) What is the probability that among 18 randomly observed individuals, exactly 5 do not cover their mouth
when sneezing?
Using the binomial distribution, the probability is 0.2050.
(Round to four decimal places as needed.)
(b) What is the probability that among 18 randomly observed individuals, fewer than 6 do not cover their
mouth when sneezing?
Using the binomial distribution, the probability is
(Round to four decimal places as needed.)
Solution
Recommended textbooks for you


Calculus For The Life Sciences
Calculus
ISBN:
9780321964038
Author:
GREENWELL, Raymond N., RITCHEY, Nathan P., Lial, Margaret L.
Publisher:
Pearson Addison Wesley,

Holt Mcdougal Larson Pre-algebra: Student Edition…
Algebra
ISBN:
9780547587776
Author:
HOLT MCDOUGAL
Publisher:
HOLT MCDOUGAL


Calculus For The Life Sciences
Calculus
ISBN:
9780321964038
Author:
GREENWELL, Raymond N., RITCHEY, Nathan P., Lial, Margaret L.
Publisher:
Pearson Addison Wesley,

Holt Mcdougal Larson Pre-algebra: Student Edition…
Algebra
ISBN:
9780547587776
Author:
HOLT MCDOUGAL
Publisher:
HOLT MCDOUGAL
