Question
A 19-μC point charge is moving along the x-axis as shown at a speed of 16.5 × 106 m/s. The point P shown has coordinates (0.65,1.3,0) m. Note that in this figure, the z-axis is positive out of the screen.
(a) What is the x-component of the magnetic field at the point P due to the charge, in tesla?
(b) What is the y-component of the magnetic field at the point P due to the charge, in tesla?
(c) What is the z-component of the magnetic field at the point P due to the charge, in tesla?
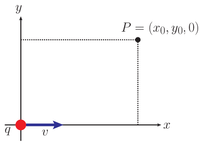
Transcribed Image Text:### Understanding Vector Components in a 2D Coordinate System
In this diagram, we have a 2D coordinate system with the x-axis and y-axis labeled. The origin point \( q \) is marked with a red dot and is labeled 'q'.
- **Vector \( \mathbf{v} \)**: This vector originates from the point \( q \) and extends horizontally along the x-axis. It is represented by a blue arrow pointing to the right.
- **Point \( P \)**: This point is denoted as \( P = (x_0, y_0, 0) \), implying the coordinates of point \( P \) in the 2-dimensional space where the z-coordinate is zero. Point \( P \) is marked with a black dot on the graph.
- **Dashed Lines**: The figure includes horizontal and vertical dashed lines extending from point \( P \) to the x-axis and y-axis, respectively. These lines help in identifying the exact coordinates of point \( P \) by forming right angles with the axes.
The diagram effectively illustrates the relationship between the origin point \( q \) and another point \( P \) in the 2D plane, accompanied by the vector \( \mathbf{v} \) starting at \( q \) and moving horizontally along the x-axis. This representation helps in understanding the positioning and vectorial relationships in the coordinate system.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps with 1 images

Knowledge Booster
Similar questions
- A 8-μC point charge is moving along the x-axis as shown at a speed of 11.5 × 106 m/s. The point P shown has coordinates (0.75,1.9,0) m. Note that in this figure, the z-axis is positive out of the screen. What is the z-component of the magnetic field at point P due to the charge in tesla?arrow_forwardFields of an electron At a particular instant a proton is at the origin, moving with velocity m/s. At this instant: (a) What is the electric field at location m, due to the proton? E = N/C (b) What is the magnetic field at the same location due to the proton? B = <arrow_forwardA particle having mass m = 2.80E-4 kg carries a negative charge q= −1.70E-6 C . The particle is given an initial velocity in the −y direction (downward), as shown in the figure, of v = 7.84E2 m/s. Everywhere in space there is a uniform constant magnetic field B = 0.340 T pointing in the +z direction, which is out of the plane of the page. What is the speed of the particle after 7 periods of the cyclotron motion (in m/s)?arrow_forward
- What is the magnitude of the magnetic field at point “P" which is located at a dis- tance of 0.50 m from the z axis? (in µT)arrow_forwardWhen the magnetic field is into the page (X), is that negative z direction, and when the magnetic field is out of the page (.), is that positive z direction?arrow_forwardThe two wires shown in the figure below are separated by d = 11.1 cm and carry currents of I = 4.90 A in opposite directions. 2d- (a) Find the magnitude and direction of the net magnetic field at a point midway between the wires. magnitude µT direction --Select--- (b) Find the magnitude and direction of the net magnetic field at point P,, 11.1 cm to the right of the wire on the right. magnitude direction |---Select--- (c) Find the magnitude and direction of the net magnetic field at point Pa, 2d = 22.2 cm to the left of the wire on the left. magnitude uT direction ---Select---arrow_forward
- Using the magnetic moment, you found to calculate the current using µ =N I (Area). Take the radius of the circular loop as 0.01 meters in order to calculate its area. My magnetic moment is 2.00E-8 All my data is attached please find the area and currentarrow_forwardAn electron is launched at a speed of v at an angle of 0 north of east into a region with a uniform magnetic field. The magnitude of the magnetic field is B and the field is pointing due east. a) Find the radius of curvature of the trajectory. b) Find the pitch (the distance traveled during one revolution, perpendicular to the plane of circular motion) of the trajectory.arrow_forwardA short current element di = (0.500 mm) carries a current of 5.30 A in the same direction as di Point P is located at 7 = (-0.730 m)i + (0.390 m)k. Find the magnetic field at P produced by this current element. Enter the x, y, and z components of the magnetic field in teslas separated by commas. dBx, dBy, dB₂ = VE ΑΣΦ ? Tarrow_forward
- A circular current of 20.0 A is inscribed within a square current of 34.8 A in the plane of the page. What is the net magnetic field at the center of the system if both currents are in the same directon given the radius of the circle is 0.045m? Answer with a number measured in micro Teslaarrow_forwardA particle having mass m = 2.80E-4 kg carries a negative charge q= −1.70E-6 C . The particle is given an initial velocity in the −y direction (downward), as shown in the figure, of v = 7.84E2 m/s. Everywhere in space there is a uniform constant magnetic field B = 0.340 T pointing in the +z direction, which is out of the plane of the page. What is the speed of the particle after 7 periods of the cyclotron motion (in m/s)?arrow_forwardtake ur time plsarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios