a. Find the amplitude, midline, and period of h(t). Enter the exact answers. Amplitude: A= meters Midline: h= meters Period: P= minutes b. Assume that a person has just boarded the Ferris wheel from the platform and that the Ferris wheel starts spinning at time t=0. Find a formula for the height function h(t). Hints: What is the value of h(0)? Is this the maximum value of h(t), the minimum value of h(t), or a value between the two? The function sin(t) has a value between its maximum and minimum at t=0 , so can h(t) be a straight sine function? The function cos(t) has its maximum at t=0, so can h(t) be a straight cosine function? c. If the Ferris wheel continues to turn, how high off the ground is a person after 60 minutes?
Solve the problems below. Copy the description of your Ferris wheel in the text box and include that as part of your initial Discussion post in Brightspace. Using "copy" from here in Mobius and "paste" into Brightspace should work.
Hint: This is similar to Question 48 in Section 8.1 of our textbook. We covered this section in "5-1 Reading and Participation Activities: Graphs of the Sine and Cosine Functions" in Module Five. You can check your answers to part a and c to make sure that you are on the right track.
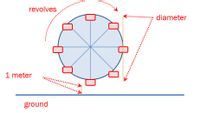
Please use the image provided to help with the above questions
A Ferris wheel is 21 meters in diameter and completes 1 full revolution in 16 minutes.
A Ferris wheel is 21 meters in diameter and boarded from a platform that is 1 meter above the ground. The six o’clock position on the Ferris wheel is level with the loading platform. The wheel completes 1 full revolution in 16 minutes. The function h(t) gives a person’s height in meters above the ground t minutes after the wheel begins to turn.
a. Find the amplitude, midline, and period of h(t).
Enter the exact answers.
Amplitude: A= meters
Midline: h= meters
Period: P= minutes
b. Assume that a person has just boarded the Ferris wheel from the platform and that the Ferris wheel starts spinning at time t=0. Find a formula for the height function h(t).
Hints:
- What is the value of h(0)?
- Is this the maximum value of h(t), the minimum value of h(t), or a value between the two?
- The function sin(t) has a value between its maximum and minimum at t=0 , so can h(t) be a straight sine function?
- The function cos(t) has its maximum at t=0, so can h(t) be a straight cosine function?
c. If the Ferris wheel continues to turn, how high off the ground is a person after 60 minutes?
Trending now
This is a popular solution!
Step by step
Solved in 4 steps
