
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
Identify the quadratic function using the graphs below. The other picture is an example of it.
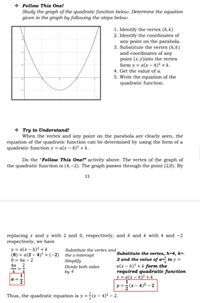
Transcribed Image Text:* Follow This One!
Study the graph of the quadratic function below. Determine the equation
given in the graph by following the steps below.
1. Identify the vertex (h, k)
2. Identify the coordinates of
any point on the parabola.
3. Substitute the vertex (h, k)
and coordinates of any
point (x,y)into the vertex
form y = a(x - h)² + k.
4. Get the value of a.
5. Write the equation of the
quadratic function.
* Try to Understand!
When the vertex and any point on the parabola are clearly seen, the
equation of the quadratic function can be determined by using the form of a
quadratic function y = a(x – h)² + k.
Do the "Follow This One!" activity above. The vertex of the graph of
the quadratic function is (4, –2). The graph passes through the point (2,0). By
11
replacing x and y with 2 and 0, respectively, and h and k with 4 and -2
respectively, we have
y = a(x – h)² + k
(0) = a(2 – 4)² +(-2)
0 %3D 4а — 2
4а 2
Substitute the vertex and
Substitute the vertex, h=4, k=-
2 and the value of a=̟ to y =
a(x – h)² + k form the
required quadratic function
y = a(x – h)² + k
the x-intercept
Simplify
Divide both sides
-=
by 4
1
a =
2
y = ;
r– 4)² – 2
Thus, the quadratic equation is y ==(x – 4)² – 2.
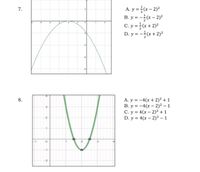
Transcribed Image Text:A. y =(x – 2)2
B. y = -(x – 2)?
C. y = « + 2)*
D. y = -(x + 2)²
7.
-3
A. y = -4(x +2)² + 1
B. y = -4(x – 2)² – 1
C. y = 4(x – 2)² +1
D. y = 4(x – 2)² – 1
8.
2.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Similar questions
- Find an example of a quadratic function in the field of your interest. Draw its picture in the coordinate plane. Find its vertex, x-intercept(s), y-intercept, and max or min value and explain what they represent in your problemarrow_forwardiPhone Sales The table lists the number of iPhones sold in millions in the first 5 years on the market. Find a quadratic function f that models the data. Year 1 2 3| 4 5 Units sold 1 20 | 50 | 100| 180| Source: Business Insider.arrow_forwardThe graph shows a quadratic function of the form R(t) = at2+bt+c, which represents the yearly revenue for a company, where R(t) is the revenue in year t. a. Is the value of a positive, negative, or zero? Explain. b. Write an expression in terms of a and b that represents the year t when the company had the least revenue. c. The company made the same yearly revenues in 2008 and 2018. Estimate the year in which the company had the least revenue. d. Assume that the model is still valid today. Are the yearly revenues currently increasing, decreasing, or constant? Explain.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

