Homework Help is Here – Start Your Trial Now!
Math
Advanced Math
a. Let In = strate that exp (nx) sin (exp (x)) dx. By making an appropriate substitution, or otherwise, demon- In exp ((n − 1)x) cos (exp (x)) + (n − 1) exp ((n − 2)x) sin (exp (x)) — (n − 1) (n − 2) In-2. b. Hence, or otherwise, compute exp (6x) sin (exp (x)) dx. ==

a. Let In = strate that exp (nx) sin (exp (x)) dx. By making an appropriate substitution, or otherwise, demon- In exp ((n − 1)x) cos (exp (x)) + (n − 1) exp ((n − 2)x) sin (exp (x)) — (n − 1) (n − 2) In-2. b. Hence, or otherwise, compute exp (6x) sin (exp (x)) dx. ==

Calculus For The Life Sciences
Calculus For The Life Sciences
2nd Edition
ISBN:9780321964038
Author:GREENWELL, Raymond N., RITCHEY, Nathan P., Lial, Margaret L.
Publisher:GREENWELL, Raymond N., RITCHEY, Nathan P., Lial, Margaret L.
Chapter6: Applications Of The Derivative
Section6.3: Implicit Differentiation
Problem 44E
See similar textbooks
icon
Related questions
Question
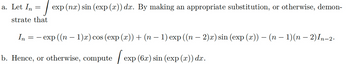
= J exp (nx) sin (exp (x)) dx. By making an appropriate substitution, or otherwise, demon- strate that a. Let In In = - exp ((n − 1)x) cos (exp (x)) + (n − 1) exp ((n − 2)x) sin (exp (x)) - (n − 1)(n − 2) In-2. b. Hence, or otherwise, compute exp (6x) sin (exp (x)) dx .
Transcribed Image Text:= J exp (nx) sin (exp (x)) dx. By making an appropriate substitution, or otherwise, demon- strate that a. Let In In = - exp ((n − 1)x) cos (exp (x)) + (n − 1) exp ((n − 2)x) sin (exp (x)) - (n − 1)(n − 2) In-2. b. Hence, or otherwise, compute exp (6x) sin (exp (x)) dx .
Expert Solution
steps

Step by step

Solved in 3 steps

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question

Can you write it? I don't understand typing it.

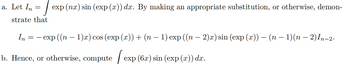
= J exp (nx) sin (exp (x)) dx. By making an appropriate substitution, or otherwise, demon- strate that a. Let In In = - exp ((n − 1)x) cos (exp (x)) + (n − 1) exp ((n − 2)x) sin (exp (x)) - (n − 1)(n − 2) In-2. b. Hence, or otherwise, compute exp (6x) sin (exp (x)) dx .
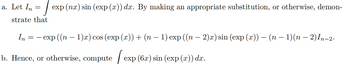
Transcribed Image Text:= J exp (nx) sin (exp (x)) dx. By making an appropriate substitution, or otherwise, demon- strate that a. Let In In = - exp ((n − 1)x) cos (exp (x)) + (n − 1) exp ((n − 2)x) sin (exp (x)) - (n − 1)(n − 2) In-2. b. Hence, or otherwise, compute exp (6x) sin (exp (x)) dx .
Solution
Bartleby Expert
SEE SOLUTION
Recommended textbooks for you
Calculus For The Life Sciences
Calculus For The Life Sciences
Calculus
ISBN:
9780321964038
Author:
GREENWELL, Raymond N., RITCHEY, Nathan P., Lial, Margaret L.
Publisher:
Pearson Addison Wesley,
Algebra & Trigonometry with Analytic Geometry
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage
SEE MORE TEXTBOOKS