a. Find all the intersection points of the following curves. b. Find the area of the entire region that lies within both curves. r = 23+23 sin 0 and r= 23+23 cos 0 a. Identify all the intersection points. Use 0 for the 0 coordinate of the pole if it's an intersection point. (Type an ordered pair. Type the coordinate for 0 in radians. Use a comma to separate answers as needed. Type an exact answer, using as needed.)
a. Find all the intersection points of the following curves. b. Find the area of the entire region that lies within both curves. r = 23+23 sin 0 and r= 23+23 cos 0 a. Identify all the intersection points. Use 0 for the 0 coordinate of the pole if it's an intersection point. (Type an ordered pair. Type the coordinate for 0 in radians. Use a comma to separate answers as needed. Type an exact answer, using as needed.)
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
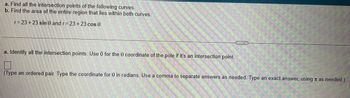
Transcribed Image Text:### Problem Overview
**Objective:**
- a. Determine all intersection points of the given polar curves.
- b. Calculate the area enclosed by both curves.
**Given Curves:**
- \( r = 23 + 23 \sin \theta \)
- \( r = 23 + 23 \cos \theta \)
### Part a: Finding Intersection Points
**Instructions:**
Identify all intersection points. Use \( 0 \) for the \( \theta \) coordinate at the pole if it is an intersection point.
**Input Format:**
- Type an ordered pair for \( \theta \) in radians.
- Use a comma to separate answers as needed.
- Provide exact answers using \(\pi\) as needed.
### Part b: Calculating Enclosed Area
Determine the area of the entire region that lies within both curves.
### Notes
- Ensure your solutions consider the symmetries and periodic nature of sine and cosine in polar coordinates.
- This problem involves matching radii and considering the angles where these functions equal each other.
- Remember that polar curves can intersect at multiple points, including diametrically opposite angles for \(\theta\).
Expert Solution
Step 1: Given information
Step by step
Solved in 4 steps with 4 images
Recommended textbooks for you
Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education
Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY
Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education
Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY
Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,
