(a) y = r³ + 3x (c) y = 5 – 6 (b) y = 9x + x³ + 4x (d) y = 5 – 26 (x > 0) %3D
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
100%
I need help solving 7.3.1
a) c) d) f) g) h)

Transcribed Image Text:Hence explain, without using calculus, why ƒ is a monotonic function.
eakly monotonic functic
class of functions which includes the strictly increa
reasing functions and functions whose graphs have some rising and so
sections.
horizona
number of values of x, then f is strictly increasing.
T < x2. A differentiable function f is non-increasing if and only if f'(x) <0 for all
A non-increasing or non-decreasing function is said to be weakly monotonic.
Exercises
7.3.1 Which of the following functions are monotonic? Which are weakly monotonic?
In each case, the domain of the function is R unless otherwise stated.
(a) y = r³ + 3x
(c) y = 5 – 26
(e) y = 3/(1+x*)
(8) y = x + |a|
(b) y = 9x + x³ + 4x
(d) y = 5 – a6 (x > 0)
(f) y = (x+1)/(x – 1) (x > 1)
(h) y%3D 2x + \미|
7.3.2 In each of the following cases, find the range of values of the constant a for which
the function f(x) is monotonic.
(a) f(x) = (x+ a)³ – 80x (x E R);
(b) f(x) = (x+a)% – 80x (x> 0);
(c) f(x) = (x+ a)-2 + 80x (x > 0).
7.3.3 As in panel (D) of Figure 7.1, let
2x
f(x)
(-1 < x < 1).
x2 - 1
Show that, for all such r,
1
f(a)
1
1+ x
1- x
Expert Solution
Step 1
Note: we answer up-to 3 multiple subparts. Please resubmit question which you would like to get answered.
a) Given function is
Draw graph of given function.
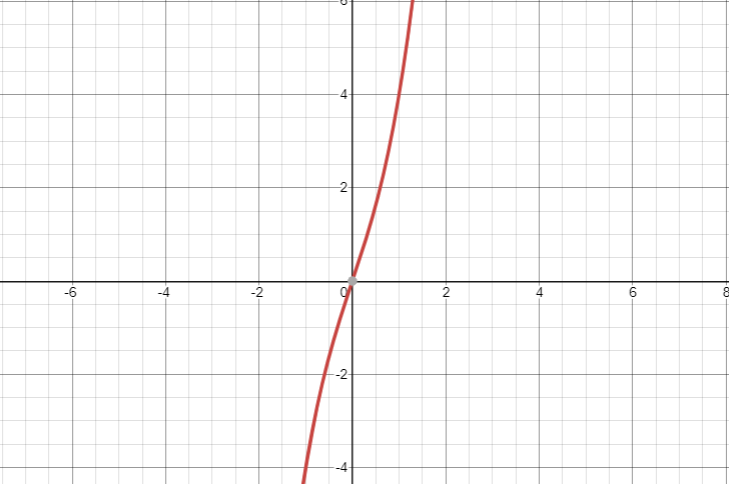
It is clearly visible from the graph with increase in value of 'x', value of 'y' increases as well. Therefore, given function is monotonic increasing over .
Step by step
Solved in 3 steps with 3 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

