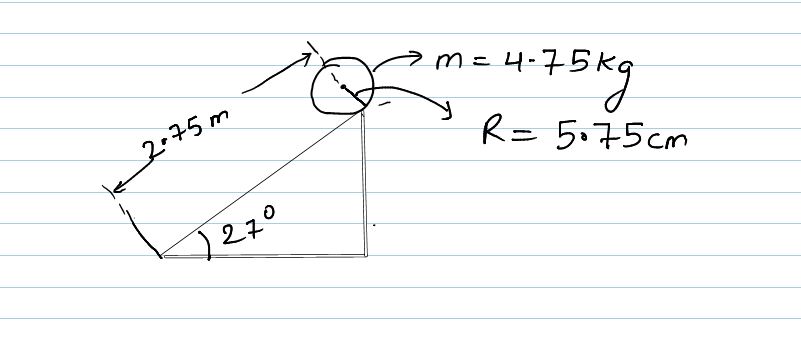
A uniform, solid sphere of radius 5.75 cm and mass 4.75 kg starts with a purely translational speed of 1.75 m/s at the top of an inclined plane. The surface of the incline is 2.75 m long, and is tilted at an angle of 27.0∘ with respect to the horizontal. Assuming the sphere rolls without slipping down the incline, calculate the sphere's final translational speed v2 at the bottom of the ramp.
A uniform, solid sphere of radius 5.75 cm and mass 4.75 kg starts with a purely translational speed of 1.75 m/s at the top of an inclined plane. The surface of the incline is 2.75 m long, and is tilted at an angle of 27.0∘ with respect to the horizontal. Assuming the sphere rolls without slipping down the incline, calculate the sphere's final translational speed v2 at the bottom of the ramp.
This is problem belong to dynamics of rigid body.
When solid sphere comes down the plane it losses its potential energy and gain in kinetic energy( both rotational and translations kinetic energy).
(assume there is no slipping down the plane) motion of solid sphere will look like as shown in figure
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 1 images
