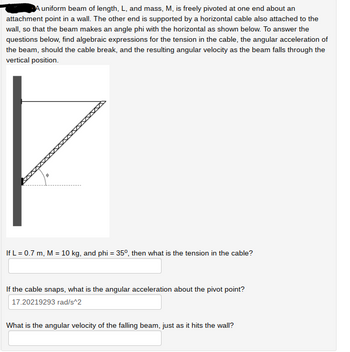
A uniform beam of length, L, and mass, M, is freely pivoted at one end about an attachment point in a wall. The other end is supported by a horizontal cable also attached to the wall, so that the beam makes an angle phi with the horizontal as shown below. To answer the questions below, find algebraic expressions for the tension in the cable, the angular acceleration of the beam, should the cable break, and the resulting angular velocity as the beam falls through the vertical position.

In the figure, a constant horizontal force The wheel rolls smoothly on the horizontal surface, and the acceleration of its center of mass has magnitude 0.82 m/s2. (a) What is the magnitude of the frictional force on the wheel? (b) What is the rotational inertia of the wheel abeut the rotation axis through its center of mass? of magnitude 12 N is applied to a wheel of mass 7.8 kg and radius 0.27 m. app (a) Number Units N 6.2 (b) Number 0.683 Units kg m^2 Click if you would like to Show Work for this question: Open Show Work y Policy © 2000-2020 John Wiley & Sons, Inc. All Rights Reserved. A Division of John Wiley & Sons, Inc. Version 4.24.20.1

The uniform solid block in the figure has mass 27.6 kg and edge lengths a = 0.971 m, b = 1.43 m, and c = 0.118 m. Calculate its rotational inertia about an axis through one corner and perpendicular to the large faces. Rotation SEXE Number Units rad rad/s rad/s^2 kg-m^2 N-m kg-m^2/s rad^2/s^2 Save for Later Attempts: 0 of 5 used Submit Answer Using multiple attempts will impact your score. 20% score reduction after attempt 4

The outstretched hands and arms of a figure skater preparing for a spin can be considered a slender rod pivoting about an axis through its center ( Ibar=ml² where l is the length of the bar). When the skater's hands and arms are brought in and wrapped around their body to execute the spin, the hands and arms can be considered a thin-walled hollow cylinder. The hands and arms have a combined mass 10 kg. When outstretched, they span 2.1 m. When wrapped, they form a cylinder of radius 21 cm. The moment of inertia about the rotation axis of the remainder of the body is constant and equal to 0.6 kg-m2. If the original angular speed is 0.5 rev/s, what is the final angular speed? 00f= rev/s Determine how much the figure skater's rotational KE increased. [NOTE: We express energy in J. To get J, you must convert your angular velocities to the appropriate mks. units which are rad/s.] ΔΚΕ- =

A uniform beam of length, L, and mass, M, is freely pivoted at one end about an attachment point in a wall. The other end is supported by a horizontal cable also attached to the wall, so that the beam makes an angle phi with the horizontal as shown below. To answer the questions below, find algebraic expressions for the tension in the cable, the angular acceleration of the beam, should the cable break, and the resulting angular velocity as the beam falls through the vertical position. If L = 1.8 m, M = 15 kg, and phi = 30o, then what is the tension in the cable? If the cable snaps, what is the angular acceleration about the pivot point? What is the angular velocity of the falling beam, just as it hits the wall?

Two wheels have the same mass and radius of 4.9kg and 0.45 m, respectively. One has (a) the shape of a hoop and the other (b) the shape of a solid disk. The wheels start from rest and have a constant angular acceleration with respect to a rotational axis that is perpendicular to the plane of the wheel at its center. Each turns through an angle of 13 rad in 8.4 s. Find the net external torque that acts on each wheel.

A cylinder is rotating about an axis that passes through the center of each circular end piece. The cylinder has a radius of 0.110 m, an angular speed of 64.0 rad/s, and a moment of inertia of 1.08 kg-m². A brake shoe presses against the surface of the cylinder and applies a tangential frictional force to it. The frictional force reduces the angular speed of the cylinder by a factor of 9 during a time of 8.00 s. (a) Find the magnitude of the angular deceleration of the cylinder. (b) Find the magnitude of the force of friction applied by the brake shoe. (a) Number i (b) Number i Units Units

A uniform disc of mass 3.0 kg and radius 25 cm is mounted on a fixed horizontal axle. A block with mass 1.8 kg hangs from a light cord that is wrapped around the rim of the disc. What is the angular acceleration of the disc?

A 2.00-m long rod is hinged at one end. The rod is initially held in the horizontal position, and then released as the free end is allowed to fall. (a) What is the angular acceleration as it is released? (b) What is the angular acceleration when it reaches the vertical position? (c) Which position has the maximum angular velocity (vertical or horizontal)? (d) Which position has the maximum angular acceleration (vertical or horizontal)? (The moment of inertia of a rod about one end is ML2/3.)

The uniform solid block in the figure has mass 39.8 kg and edge lengths a = 0.902 m, b = 1.67 m, and c = 0.141 m. Calculate its rotational inertia about an axis through one corner and perpendicular to the large faces. Number:   Unit: