
Elements Of Electromagnetics
7th Edition
ISBN: 9780190698614
Author: Sadiku, Matthew N. O.
Publisher: Oxford University Press
expand_more
expand_more
format_list_bulleted
Question
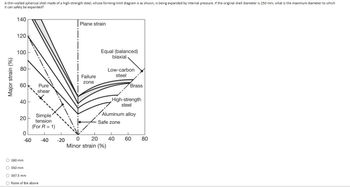
Transcribed Image Text:**Educational Content:**
### Forming-Limit Diagram for High-Strength Steel
A thin-walled spherical shell made of high-strength steel is analyzed using the forming-limit diagram shown below. This shell is being expanded by internal pressure. Given that the original shell diameter is 250 mm, determine the maximum diameter to which it can safely be expanded.
**Graph Explanation:**
The graph is a Forming-Limit Diagram that plots Major Strain (%) against Minor Strain (%).
- **Major Strain Axis (Vertical):** This axis ranges from 0% to 140%.
- **Minor Strain Axis (Horizontal):** This axis ranges from -60% to 80%.
**Regions and Lines:**
- **Plane Strain Line:** Indicating a condition where deformation is only in the major strain direction.
- **Pure Shear Line:** Shows shear deformation conditions.
- **Simple Tension Line (For R = 1):** Represents conditions under simple tension.
- **Failure Zone:** The area above the material-specific lines where failure occurs.
- **Safe Zone:** The area below the material-specific lines where the material can be safely formed.
**Material Lines:**
- **Low-Carbon Steel:** Upper middle line.
- **Brass:** Slightly below the line for low-carbon steel.
- **High-Strength Steel:** In the central zone.
- **Aluminum Alloy:** Lower zone near the safe region.
**Design Conditions:**
- **Equal (Balanced) Biaxial Line:** Indicates balanced stretching in biaxial directions.
**Possible Answers for Maximum Diameter:**
- 280 mm
- 350 mm
- 367.5 mm
- None of the Above
The solution involves determining where the high-strength steel line intersects the safe zone under the specific conditions presented.
This diagram is a critical tool in assessing the forming capability of materials under various loading conditions and is extensively used in engineering applications to prevent structural failure during the forming process.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 4 steps with 1 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- solve all 3arrow_forward1. A part made of Aluminum 6061-T6 has a yield strength = 400 MPa. For each stress state below, draw all 3 Mohr's circles, find the principal stresses, and calculate the safety factor against yield using both the distortion-energy (von Mises) and maximum shear stress (Tresca) criterions. (If relevant) A clearly labeled diagram (or diagrams) clearly pertaining to your analysis with a coordinate system and relevant labels. Final answer with appropriate units and significant figures. You can use the fprintf() command in MATLAB to format numerical results A 2-3 sentence reflection on your answer. Does it make sense? Why or why not? What are some implications?arrow_forwardThe principal plane stresses and associated strains in a 35 ksi, 02 = 15 ksi, plane at a point are 01 1 €1 = 1.02(10-3), 2 = 0.180(10-³). ▼ Determine the modulus of elasticity. Express your answer using three significant figures and include the appropriate units. E= Submit Part B V= μA Value Request Answer Submit Determine the Poisson's ratio. Express your answer using three significant figures. ΠΑΠΙ ΑΣΦ | Η VE Units Request Answer ? vec POSSIA space ?arrow_forward
- The tube has a length of 2 m and is made of the material with the properties provided in the following figure. (a) Determine the torque needed to just cause the maximum strain to reach 0.015. (b) What is the permanent angle of twist of the tube when this torque is removed?arrow_forwardThe stresses on the surface of a hard bronze component are shown in the figure below. The yield strength of the bronze is σY = 345 MPa.a) What is the factor of safety predicted by the maximum-shear-stress theory of failure for the stress state shown? Does the component fail according to this theory?b) What is the value of the Mises equivalent stress for the given state of plane stress?c) What is the factor of safety predicted by the failure criterion of the maximum-distortion energy theory of failure? Does the component fail according to this theory?arrow_forwardDerive the following equation for computing shear stress in a solid bar along an oblique plane with angle B with respect to the vertical plane. The bar is subjected to centric axial loading. sin 0 cos 0 T = Aoarrow_forward
- Parrow_forward(30%) A circular aluminum tube subjected to T pure torsion by torques T has an outer radius r2 equal to 2 times the inner radius r1. (a) If the maximum shear strain in the tube is measured as 500x10-6 rad, what is the shear strain y1 at the inner surface? (b) If the maximum allowable rate of twist (0) is 0.15°/m and the maximum shear strain is to be kept at 500x10-6 rad by adjusting the torque T, what is the minimum required outer radius (r2 )min?arrow_forward5. Consider a cylindrical specimen of a steel alloy (Figure 6.22) 10 mm in diameter and 75 mm long that is pulled in tension. Determine its elongation when a load of 20,000 N is applied. Stress (MPa) 600 500 400 300 200 100 0 0.00 0.04 Stress (MPa) 500 400 300 200 100 0.000 0.002 0.004 0.006 0.08 Strain Strain 0.12 0.16 0.20 Figure 6.22 Tensile stress-strain behavior for a steel alloy.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY

Elements Of Electromagnetics
Mechanical Engineering
ISBN:9780190698614
Author:Sadiku, Matthew N. O.
Publisher:Oxford University Press

Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:9780134319650
Author:Russell C. Hibbeler
Publisher:PEARSON

Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:9781259822674
Author:Yunus A. Cengel Dr., Michael A. Boles
Publisher:McGraw-Hill Education

Control Systems Engineering
Mechanical Engineering
ISBN:9781118170519
Author:Norman S. Nise
Publisher:WILEY

Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:9781337093347
Author:Barry J. Goodno, James M. Gere
Publisher:Cengage Learning

Engineering Mechanics: Statics
Mechanical Engineering
ISBN:9781118807330
Author:James L. Meriam, L. G. Kraige, J. N. Bolton
Publisher:WILEY