
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Concept explainers
Question
thumb_up100%

Transcribed Image Text:A tank is initially filled with 400 gal of salt solution with a concentration of 0.08 lb/gal. At time
t = 0, pure water is poured into the tank at a rate of 2 gal/min. Simultaneously, a drain is opened
at the bottom of the tank allowing the solution to leave the tank at a rate of 3 gal/min. The tank
is well-stirred. Let x(t) represent the amount of salt (in lb) in the tank after t min. Write down the
initial value problem that x(t) satisfies. DO NOT SOLVE the initial value problem.
Expert Solution
arrow_forward
Step 1
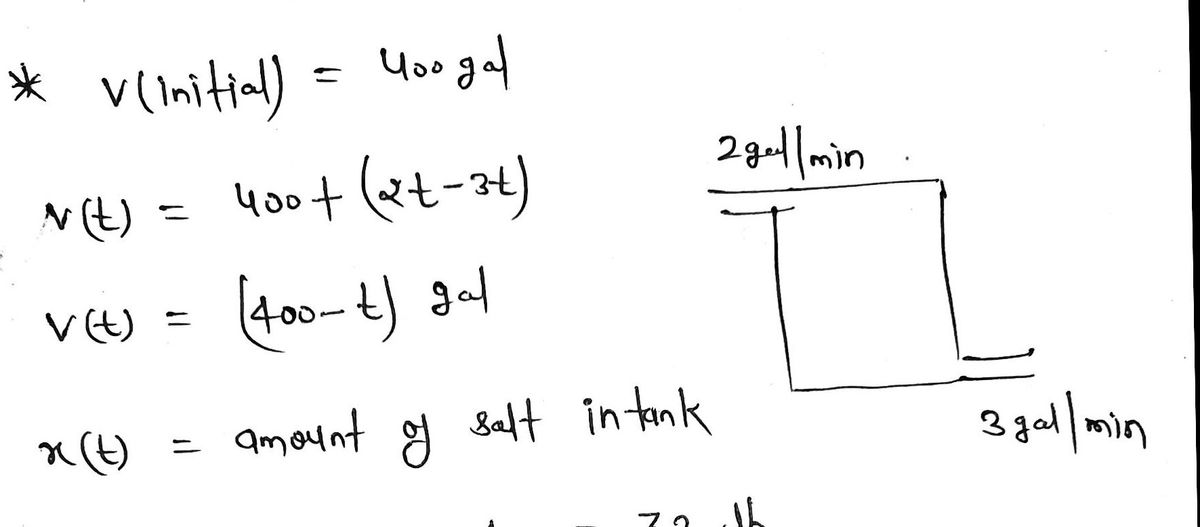
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Similar questions
- A brine solution of salt flows at a constant rate of 5 L/min into a large tank that initially held 100 L of brine solution in which was dissolved 0.25 kg of salt. The solution inside the tank is kept well stirred and flows out of the tank at the same rate. If the concentration of salt in the brine entering the tank is 0.05 kg/L, determine the mass of salt in the tank after t min. When will the concentration of salt in the tank reach 0.01 kg/L? plz help Determine the mass of salt in the tank after t min. mass= kg ■ • L G TT P More Xarrow_forwardA brine solution of salt flows at a constant rate of 6 L/min into a large tank that initially held 100 L of pure water. The solution inside the tank is kept well stirred and flows out of the tank at a rate of 5 L/min. If the concentration of salt in the brine entering the tank is 0.5 kg/L, determine the mass of salt in the tank after t min. When will the concentration of salt in the tank reach 0.4 kg/L? Determine the mass of salt in the tank after t min. mass=kgarrow_forwardIn a natural habitat, the population of a certain species of snails is given by P=0.8(Ae* +500), where A and k are constants and / is the time in years starting from 1 January 2010. Over a period of 8 years from 1 January 2010 to 31 December 2017, the population decreased from 50 000 to 19 000. (i) Calculate the valucs of A and of k.arrow_forward
- A brine solution of salt flows at a constant rate of 5 L/min into a large tank that initially held 100 L of brine solution in which was dissolved 0.15 kg of salt. The solution inside the tank is kept well stirred and flows out of the tank at the same rate. If the concentration of salt in the brine entering the tank is 0.03 kg/L, determine the mass of salt in the tank after t min. When will the concentration of salt in the tank reach 0.01 kg/L? Determine the mass of salt in the tank after t min. mass= kgarrow_forwardWe have a large tank filled with 50 liters of pure water. there is a salt solution of concentration 20 g/L flowing into the tank at a rate of 2 L/min. The well mixed solution is flowing out of the tank at a rate of 1 L/min. find the concentration of salt in the tank as a function of time. no need to worry about the tank overflowing.arrow_forwardSuppose: • The vat contains 270 gallons of liquid, which • • . never changes. Sugar water with a concentration of 10 tablespoons/gallon flows through pipe A into the vat at the rate of 30 gallons/minute. Sugar water with a concentration of 8 tablespoons/gallon flows through pipe B into the vat at the rate of 35 gallons/minute. • The liquid in the vat is kept well-mixed. Sugar water leaves the vat through pipe C at the rate of 65 gallons/minute. Let S(t) represent the number of tablespoons of sugar in the vat at time t, where t is given in minutes. (A) Write the DE model for the time rate of change of sugar in the vat: dS dt (B) Solve the differential equation to find the amount of sugar in the vat as a function of time. Your function will have an arbitrary constant K in it. Assume that K > 0. S(t) = (C) Suppose that there are 32 tablespoons of sugar in the vat at t = present 4 minutes later? 0. How many tablespoons will be tablespoonsarrow_forward
- A brine solution of salt flows at a constant rate of 3 L/min into a large tank that initially held 100 L of pure water. The solution inside the tank is kept well stirred and flows out of the tank at a rate of 2 L/min. If the concentration of salt in the brine entering the tank is 0.6 kg/L, determine the mass of salt in the tank after t min. When will the concentration of salt in the tank reach 0.5 kg/L? ... Determine the mass of salt in the tank after t min. mass= kgarrow_forwardThe rate at which a solid substance dissolves [dQ/dt] varies directly as the product of undissolved solid present (in the solvent) [A - Q] and as the difference between the saturation concentration [Cs] and the instantaneous concentration [Ci] of the substance. Let Q - the amount of the substance dissolved at any time t,Let A - the total amount of the substance, then dQ/dt = (A - Q)(Cs - Ci) Twenty pounds of salt is dumped into the tank containing 120 lb of solvent, and at the end of 22 minutes, the concentration is observed to be 1 part solute to 30 parts of solvent. Find the amount of solute that is in the solution at any time t, assuming that the saturation concentration is 1 part solute to 3 parts solvent. Answer is shown below.arrow_forwardA brine solution of salt flows at a constant rate of 4 L/min into a large tank that initially held 100 L of pure water. The solution inside the tank is kept well stirred and flows out of the tank at a rate of 3 L/min. If the concentration of salt in the brine entering the tank is 0.4 kg/L, determine the mass of salt in the tank after t min. When will the concentration of salt in the tank reach 0.2 kg/L? Determine the mass of salt in the tank after t min. mass= 4(t+100) - 4x10² (t+100³) kg Aarrow_forward
- Initially 9 grams of salt are dissolved into 7 liters of water. Brine with concentration of salt 8 grams per liter is added at a rate of 5 liters per minute. The tank is well mixed and drained at 5 liters per minute. a) Let x be the amount of salt, in grams, in the solution after t minutes have elapsed. Find a formula for the rate of change in the amount of salt, dx/dt, in terms of the amount of salt in the solution x. dx dt b) Find a formula for the amount of salt, in grams, after t minutes have elapsed. x(t) = c) How long must the process continue until there are exactly 40 grams of salt in the tank?arrow_forwardDifferentiate the function P = 10e-0.8t %3D P'arrow_forwardA brine solution of salt flows at a constant rate of 8 L/min into a large tank that initially held 100 L of brine solution in which was dissolved 0.1 kg of salt. The solution inside the tank is kept well stirred and flows out of the tank at the same rate. If the concentration of salt in the brine entering the tank is 0.02 kg/L, determine the mass of salt in the tank after t min. When will the concentration of salt in the tank reach 0.01 kg/L? Determine the mass of salt in the tank after t min. mass = kg When will the concentration of salt in the tank reach 0.01 kg/L? The concentration of salt in the tank will reach 0.01 kg/L after minutes. (Round to two decimal places as needed.)arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

