A system is being designed to remove heat from a server rack in a data center. The figure below provides a schematic of this system. A pump circulates water through a heat sink in the rack to remove 5000 W of heat. To keep the electronics below the temperature at which damage may occur, the water leaving the server rack will be limited to 80 °C. That temperature will result in the most optimal system, so you can assume that it is the temperature of the water leaving the server rack. This water is then circulated to a heat exchanger that can be modeled as a counter flow model with a stream of air to remove the heat. Air with an inlet temperature of 20 C at a mass flow rate of 0.1 kg/s is blown through this heat exchanger. Your task is to determine the size of the air-to-water heat exchanger (i.e., its area) and the mass flow rate of water to minimize the life cycle cost of the system. The cost, which is dominated by the first cost of the heat exchanger and the energy to run the pump, has been estimated to be: Cost = 45*A + 0.01*mw² Where A: area of heat exchanger mw: mass flow rate of water Other information: The U value of the heat exchanger is 40 W/(m²*K) (a) Provide the equations describing the optimization problem, including the objective function, the design variables, and any constraint equations. (b) Convert the formulation into an unconstrained optimization in a single variable (i.e., use the equations in part (a) to eliminate all but one unknown variable) (c) Use a Fibonacci search to determine the optimum settings of your design variables using the equation developed in part (b). The mass flow rate of water is expected to be between 1 kg/s and 12 kg/s, and you would like to know the optimum setting to within 0.5 kg/s.
A system is being designed to remove heat from a server rack in a data center. The figure below provides a schematic of this system. A pump circulates water through a heat sink in the rack to remove 5000 W of heat. To keep the electronics below the temperature at which damage may occur, the water leaving the server rack will be limited to 80 °C. That temperature will result in the most optimal system, so you can assume that it is the temperature of the water leaving the server rack. This water is then circulated to a heat exchanger that can be modeled as a counter flow model with a stream of air to remove the heat. Air with an inlet temperature of 20 C at a mass flow rate of 0.1 kg/s is blown through this heat exchanger. Your task is to determine the size of the air-to-water heat exchanger (i.e., its area) and the mass flow rate of water to minimize the life cycle cost of the system. The cost, which is dominated by the first cost of the heat exchanger and the energy to run the pump, has been estimated to be: Cost = 45*A + 0.01*mw² Where A: area of heat exchanger mw: mass flow rate of water Other information: The U value of the heat exchanger is 40 W/(m²*K) (a) Provide the equations describing the optimization problem, including the objective function, the design variables, and any constraint equations. (b) Convert the formulation into an unconstrained optimization in a single variable (i.e., use the equations in part (a) to eliminate all but one unknown variable) (c) Use a Fibonacci search to determine the optimum settings of your design variables using the equation developed in part (b). The mass flow rate of water is expected to be between 1 kg/s and 12 kg/s, and you would like to know the optimum setting to within 0.5 kg/s.
Elements Of Electromagnetics
7th Edition
ISBN:9780190698614
Author:Sadiku, Matthew N. O.
Publisher:Sadiku, Matthew N. O.
ChapterMA: Math Assessment
Section: Chapter Questions
Problem 1.1MA
Related questions
Question
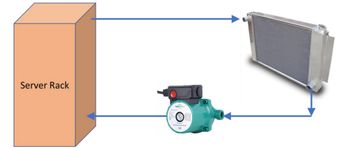
Transcribed Image Text:The image illustrates a cooling system for a server rack using a closed-loop configuration. It consists of three main components:
1. **Server Rack**: A rectangular box labeled "Server Rack," indicating where the heat is generated.
2. **Radiator**: This component is shown to the right of the server rack. It resembles a metal structure with fins, designed for heat dissipation. The radiator releases the heat transferred from the server rack.
3. **Pump**: Located below the radiator and server rack, this device circulates the coolant throughout the loop, ensuring the continuous transfer of heat away from the server rack.
**Flow of Coolant**:
- From the server rack, cooled fluid moves to the radiator, as indicated by the blue arrows pointing to the right.
- After the fluid dissipates heat in the radiator, it moves downward and enters the pump.
- The pump circulates the fluid back to the server rack, completing the cycle, as shown by the blue arrows pointing left.
This configuration maintains an efficient cooling process by circulating coolant between the server rack and the radiator.
![A system is being designed to remove heat from a server rack in a data center. The schematic provided shows the system's setup. A pump circulates water through a heat sink in the rack, removing 5000 W of heat. To prevent electronic damage, the water leaving the server rack is kept at a max temperature of 80 °C, which is considered optimal for the system. This water then circulates to a heat exchanger, modeled as a counterflow heat exchanger, where air is used to remove the heat. Air at 20 °C with a mass flow rate of 0.1 kg/s is blown through this exchanger.
The goal is to determine the optimal size for the air-to-water heat exchanger and the water's mass flow rate to minimize the system's life cycle cost. This cost, primarily from the heat exchanger's initial cost and pump energy, is given by:
\[ \text{Cost} = 45*A + 0.01*m_w^2 \]
Where:
- \( A \): area of the heat exchanger
- \( m_w \): mass flow rate of water
Additional info:
- The heat exchanger's U value is 40 W/(m²*K)
Tasks:
(a) Define the optimization problem with objective function, design variables, and constraints.
(b) Reformulate it into a single-variable optimization problem.
(c) Utilize a Fibonacci search to find optimal settings within a water mass flow rate range of 1 kg/s to 12 kg/s, accurate to 0.5 kg/s.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Ff0e69105-edad-4e40-a986-7d2af8f1b9bd%2F2a75fca7-2529-4889-872d-066006c60b9f%2Fh7tx0ye_processed.jpeg&w=3840&q=75)
Transcribed Image Text:A system is being designed to remove heat from a server rack in a data center. The schematic provided shows the system's setup. A pump circulates water through a heat sink in the rack, removing 5000 W of heat. To prevent electronic damage, the water leaving the server rack is kept at a max temperature of 80 °C, which is considered optimal for the system. This water then circulates to a heat exchanger, modeled as a counterflow heat exchanger, where air is used to remove the heat. Air at 20 °C with a mass flow rate of 0.1 kg/s is blown through this exchanger.
The goal is to determine the optimal size for the air-to-water heat exchanger and the water's mass flow rate to minimize the system's life cycle cost. This cost, primarily from the heat exchanger's initial cost and pump energy, is given by:
\[ \text{Cost} = 45*A + 0.01*m_w^2 \]
Where:
- \( A \): area of the heat exchanger
- \( m_w \): mass flow rate of water
Additional info:
- The heat exchanger's U value is 40 W/(m²*K)
Tasks:
(a) Define the optimization problem with objective function, design variables, and constraints.
(b) Reformulate it into a single-variable optimization problem.
(c) Utilize a Fibonacci search to find optimal settings within a water mass flow rate range of 1 kg/s to 12 kg/s, accurate to 0.5 kg/s.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 4 steps with 7 images
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Recommended textbooks for you
Elements Of Electromagnetics
Mechanical Engineering
ISBN:
9780190698614
Author:
Sadiku, Matthew N. O.
Publisher:
Oxford University Press
Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:
9780134319650
Author:
Russell C. Hibbeler
Publisher:
PEARSON
Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:
9781259822674
Author:
Yunus A. Cengel Dr., Michael A. Boles
Publisher:
McGraw-Hill Education
Elements Of Electromagnetics
Mechanical Engineering
ISBN:
9780190698614
Author:
Sadiku, Matthew N. O.
Publisher:
Oxford University Press
Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:
9780134319650
Author:
Russell C. Hibbeler
Publisher:
PEARSON
Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:
9781259822674
Author:
Yunus A. Cengel Dr., Michael A. Boles
Publisher:
McGraw-Hill Education
Control Systems Engineering
Mechanical Engineering
ISBN:
9781118170519
Author:
Norman S. Nise
Publisher:
WILEY
Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:
9781337093347
Author:
Barry J. Goodno, James M. Gere
Publisher:
Cengage Learning
Engineering Mechanics: Statics
Mechanical Engineering
ISBN:
9781118807330
Author:
James L. Meriam, L. G. Kraige, J. N. Bolton
Publisher:
WILEY