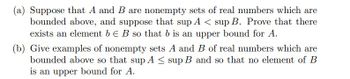
(a) Suppose that A and B are nonempty sets of real numbers which arebounded above, and suppose that sup A < sup B. Prove that thereexists an element b E B so that b is an upper bound for A.(b) Give examples of nonempty sets A and B of real numbers which arebounded above so that sup A ≤ sup B and so that no element of Bis an upper bound for A.

(a) Suppose that A and B are nonempty sets of real numbers which are bounded above, and suppose that…

Answered: (a) Suppose that A and B are nonempty…

Advanced Engineering Mathematics

10th Edition

ISBN:9780470458365

Author:Erwin Kreyszig

Publisher:Erwin Kreyszig

Chapter2: Second-order Linear Odes

Section: Chapter Questions

Problem 1RQ

See similar textbooks

Similar questions

Show that for any real number x and a subset A of R, exactly one of the following holds: (a) x is an interior point of A, (b) x is a boundary point of A or (c) 푥 is an exterior point of A.
(a) Suppose a, de N. Define what it means to say that d divides a. (b) Find all natural numbers d such that d | 24 but d | 30. (c) Suppose a, b, d E N and that d | a and d | b. Prove that d | a² + b. (d) Suppose X is a non-empty set of real numbers. Define what is meant by an upper bound for X. If X has an upper bound, define what is meant by a supremum for X. (e) Let -{n-1: EN}. {" X = Find (with proof) the supremum of X.
It was noted that the binary propositional operators, A and V, can be regarded as functions, f: B x B B. Explain why there exist 16 such functions in all.
Given any set of 15 integers, must there be two that have the sameremainder when divided by 12? Prove using the pigeonhole principle. Eitherdescribe the pigeons, the pigeonholes, and how the pigeons get to the pigeonholes, or describe a function by giving its domain, co-domain, and how elements of the domain are related to elements of the co-domain.
prove that or give a counter example , every set of negative real numbers has a supremum.
Suppose that c is a positive integer. Definef(c) to be the number of pairs (a, b) ofpositive integers with c < a < b for whichtwo circles of radius a, two circles of radius b,and one circle of radius c can be drawn sothat• each circle of radius a is tangent to bothcircles of radius b and to the circle ofradius c, and• each circle of radius b is tangent to bothcircles of radius a and to the circle ofradius c,as shown. Determine all positive integers cfor which f(c) is even.
Does there exist a 1-1 and onto function that maps the integers to the rationales? Choose the best response below. Yes, but the function is not easily written in a "normal" way. Yes, and thus you can easily write it explicitly. No, because you can't write it explictly. No because the two set don't have the same cardinality.
Without proving anything, determine if the following statements are true or false. For any false statements, give an counterexample. (a) A finite, nonempty set of real numbers always contains its supremum. (b) If a < L for every element a in the set A, then sup A < L. (c) If A and B are sets with the property that a < b for every a E A and b e B, then sup A < inf B. (d) If sup A = s and sup B = t, then sup(A+ B) = s+t. Here and elsewhere, the set A+B is defined as A+B = {a+b:a € A, and b e B}. (e) If sup A < sup B then there is an element of B that is an upper bound for A.
a) It is known that Q ͠ N (Rational Numbers have the same power as the Natural Numbers set N.). So show that QxQ ͠ N. ( QxQ have the same power as the N ) (Definition: Let A and B be two sets.If there is a one-to-one function from A to B and at least one overlying function, it is said that A set has the same power as set B. and shown to be A ͠ B) (It's abstract mathematics, please can you write step-by-step solutions I have a shortcoming in this regard.)
A number r ∈ R is called algebraic provided for some n ∈ N there exists numbers a0, a1, … , an ∈ Z such that r satisfies p( r ) = 0 where p ( x ) = a0 + a1x + a2x2 + ⋯ + anxn. A number r ∈ R is called transcendental provided it is NOT algebraic prove the set of ALL algebraic numbers is countable and the set of ALL transcendental numbers is uncountable.
All
Suppose that S is not an empty set, and is a set of real numbers bounded below. Let A-1 be the set of all numbers x-1 with x ∈ A.Prove that infA = -sup(A-1). (<---The negative sign before the word sup means inverse)PS: inf means least upper bound and sup means the greatest lower bound.

Recommended textbooks for you

Advanced Engineering Mathematics

Advanced Math

ISBN:

9780470458365

Author:

Erwin Kreyszig

Publisher:

Wiley, John & Sons, Incorporated

Numerical Methods for Engineers

Advanced Math

ISBN:

9780073397924

Author:

Steven C. Chapra Dr., Raymond P. Canale

Publisher:

McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…

Advanced Math

ISBN:

9781118141809

Author:

Nathan Klingbeil

Publisher:

WILEY

Advanced Engineering Mathematics

Advanced Math

ISBN:

9780470458365

Author:

Erwin Kreyszig

Publisher:

Wiley, John & Sons, Incorporated

Numerical Methods for Engineers

Advanced Math

ISBN:

9780073397924

Author:

Steven C. Chapra Dr., Raymond P. Canale

Publisher:

McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…

Advanced Math

ISBN:

9781118141809

Author:

Nathan Klingbeil

Publisher:

WILEY

Mathematics For Machine Technology

Advanced Math

ISBN:

9781337798310

Author:

Peterson, John.

Publisher:

Cengage Learning,

Basic Technical Mathematics

Advanced Math

ISBN:

9780134437705

Author:

Washington

Publisher:

PEARSON

Topology

Advanced Math

ISBN:

9780134689517

Author:

Munkres, James R.

Publisher:

Pearson,

SEE MORE TEXTBOOKS