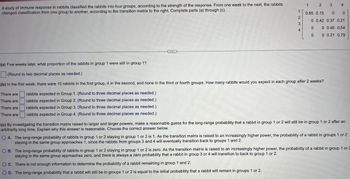
A study of immune response in rabbits classified the rabbits into four groups, according to the strength of the response. From one week to the next, the rabbits changed classification from one group to another, according to the transition matrix to the right. Complete parts (a) through (c). 1 2 3 4 0.85 0.15 0 0 2 3 4 ooo 0 0.42 0.37 0.21 0 0.46 0.54 0 0 0.21 0.79 (a) Five weeks later, what proportion of the rabbits in group 1 were still in group 1? (Round to two decimal places as needed.) (b) In the first week, there were 10 rabbits in the first group, 4 in the second, and none in the third or fourth groups. How many rabbits would you expect in each group after 2 weeks? There are There are There are There are rabbits expected in Group 1. (Round to three decimal places as needed.) rabbits expected in Group 2. (Round to three decimal places as needed.) rabbits expected in Group 3. (Round to three decimal places as needed.) rabbits expected in Group 4. (Round to three decimal places as needed.) (c) By investigating the transition matrix raised to larger and larger powers, make a reasonable guess for the long-range probability that a rabbit in group 1 or 2 will still be in group 1 or 2 after an arbitrarily long time. Explain why this answer is reasonable. Choose the correct answer below. OA. The long-range probability of rabbits in group 1 or 2 staying in group 1 or 2 is 1. As the transition matrix is raised to an increasingly higher power, the probability of a rabbit in groups 1 or 2 staying in the same group approaches 1, since the rabbits from groups 3 and 4 will eventually transition back to groups 1 and 2. OB. The long-range probability of rabbits in group 1 or 2 staying in group 1 or 2 is zero. As the transition matrix is raised to an increasingly higher power, the probability of a rabbit in group 1 or 2 staying in the same group approaches zero, and there is always a zero probability that a rabbit in group 3 or 4 will transition to back to group 1 or 2. OC. There is not enough information to determine the probability of a rabbit remaining in group 1 and 2. OD. The long-range probability that a rabbit will still be in groups 1 or 2 is equal to the initial probability that a rabbit will remain in groups 1 or 2.