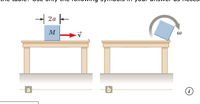
A solid block in the shape of a cube is sliding on a horizontal table with negligible friction at a speed v, as shown in figure (a) below. The block's mass is M, and the length of each side of the block is 2a. When it reaches the edge of the table, it strikes a small protruding "lip" that causes it to rotate about its lower right corner, as shown in figure (b). The collision when the block strikes the lip is inelastic. What is the minimum speed v that the block must have in order to just barely tip over and fall off the table? Use only the following symbols in your answer as necessary: M, a, and g. 2a -

Two rigid bodies, A and B, both 1 kg in mass, are connected by a linear spring with a spring constant of 0.2 N/m.  Initially, the spring is unstretched and the bodies are at rest.  If multiple forces and moments are applied to the two bodies that result in the speed of body A increasing to 10 m/s, the speed of body B increasing to 4 m/s, and the stretch of the spring increasing by 10 m, then  -20 Nm of work was done by the spring on the body A, B system. Two rigid bodies, A and B, both 1 kg in mass, are connected by a linear spring with a spring constant of 0.2 N/m.  Initially, the spring is unstretched and the bodies are at rest.  If multiple forces and moments are applied to the two bodies that result in the speed of body A increasing to 10 m/s, the speed of body B increasing to 4 m/s, and the stretch of the spring increasing by 10 m, then  -20 Nm of work was done by the spring on the body A, B system. True False

A ball is attached to one end of a wire, the other end being fastened to the ceiling. The wire is held horizontal, and the ball is released from rest (see the drawing). It swings downward and strikes a block initially at rest on a horizontal frictionless surface. Air resistance is negligible, and the collision is elastic. The masses of the ball and block are, respectively, 1.7 kg and 2.5 kg, and the length of the wire is 1.36 m. Find the velocity (magnitude and direction) of the ball just after the collision.

Kathrine lets go of a cube of mass of m = 5 kilograms on her physics demo device she created. Her cube goes down a super smooth slide surface that has a height vertical distance of h=85 cm. At the end of the slide, her cube crashes into and sticks to the lower end of a vertical pole that has a mass M=10.5 kg and length 1-2.00m. Right after the crash, the pole pivots about a hinge point near its upper end through an angle (theta) before it stops for a moment. See the image given below to visualize Katherines system. You are tasked with Figuring out the following three things The speed of her cube just before it hits the pole The angular speed of the pole just after the crash The angle (theta) through which the pole pivots a. b. C. 0 Kathrine and her device

A railroad cart with a mass of m₁ = 12.6 t is at rest at the top of an h = 10.3 m high hump yard hill. m m₂ h After it is pushed very slowly over the edge, it starts to roll down. At the bottom it hits another cart originally at rest with a mass of m₂ = 18.6 t. The bumper mechanism locks the two carts together. What is the final common speed of the two carts? (Neglect losses due to rolling friction of the carts. The letter t stands for metric ton in the SI system.)

Apollo and Artemis are playing on the teeter‑totter in their school's playground. They both have approximately the same mass. They are sitting on either side of the teeter‑totter at about the same distance from the teeter‑totter's pivot point. The teeter‑totter is going up and down and they are having a great time! Mercury, the new kid in school, wanders by. Since they are very friendly kids, Apollo and Artemis ask Mercury to join them. Mercury joins Apollo on his side of the teeter‑totter and sits next to him. What should Artemis do in order to keep the fun going? 1)Move farther from the teeter‑totter's pivot point in order to balance out the new smaller torque provided by Mercury and Apollo. 2)Move closer to the teeter‑totter's pivot point in order to balance out the new larger torque provided by Mercury and Apollo. 3)Move farther from the teeter‑totter's pivot point in order to balance out the new larger torque provided by Mercury and Apollo. 4)Move closer to the…

A physical pendulum consists of a vertical board of of mass 5.8 kg, length 172 cm, and width 5 cm hanging from a horizontal, frictionless axle. A bullet of mass 145 g and a purely horizontal speed v impacts the pendulum at the bottom edge of the board. The board then makes a complete circle. (a) If the bullet embedded itself in the board, what is the minimum speed the bullet could have to make this so? (b) If the bullet passed through the board, reducing its speed by 1/5 its original value, what is the minimum speed of the bullet? (c) If the bullet is made of rubber and rebounds elastically, what is the minimum speed the bullet could have? (d) What is the rebound speed of the bullet?

A ball is attached to one end of a wire, the other end being fastened to the ceiling. The wire is held horizontal, and the ball is released from rest (see the drawing). It swings downward and strikes a block initially at rest on a horizontal frictionless surface. Air resistance is negligible, and the collision is elastic. The masses of the ball and block are, respectively, 1.7 kg and 2.4 kg, and the length of the wire is 1.23 m. Find the velocity (magnitude and direction) of the ball (a) just before the collision, and (b) just after the collision. +y ++

A 0.450 kg ball of Play-Doh hangs from the ceiling by a string. A 0.0850 kg wad of Play-Doh is thrown straight upward from below the ball and strikes the ball with a speed of 5.60 m/s and sticks to it. (a) Is the mechanical energy of this system conserved? Yes No (b) How high (in cm) does the combined mass of Play-Doh rise above the original position of the ball of Play-Doh? X Since the collision takes place over a very short time interval, we may conserve linear momentum to obtain the speed of the combined mass right after the collision. Knowing the speed of the combined mass the instant after the collision, see if you can use your knowledge of kinematics to determine how high the combined mass rises above the original position of the ball of Play-Doh. cm

A ball with a diameter of 5 cm is released from rest and does not slip as it rolls down a curved ramp from a height of ho. The ball collides with a ramp of mass 300g connected to a spring of negligible mass. This launches the ball a vertical height of h₂ while compressing the spring 18.7 mm. With the coefficient of restitution between the ball and the ramp being 0.8, neglecting the friction between the ramp and the floor, and knowing that the ball rotates at a constant angular velocity as it is launched until It reaches h₂, find h₂. Neglect air resistance. ho OF h₂ Vball 80⁰ 3 my 18.7 mm k = 20 N/mm