Homework Help is Here – Start Your Trial Now!
Science
Advanced Physics
A small sphere with mass mm and charge qq is attached to one end of a string with length LL and tension FTFT. The other end of the string is attached to a wall which has surface-charge density σσ. The angle between the string and the wall is θθ, as shown in the drawing. a.)  Please use the interactive area below to draw the Free Body Diagram for the small sphere. (I know the diagram isn't available this way but maybe a drawing?) b.) Enter an expression for the sum of the horizontal components of the forces in the diagram in terms of the variables given in the problem statement and standard physical constants.  c.) Enter an expression for the sum of the vertical components of the forces in the diagram in terms of the variables given in the problem statement and standard physical constants.

A small sphere with mass mm and charge qq is attached to one end of a string with length LL and tension FTFT. The other end of the string is attached to a wall which has surface-charge density σσ. The angle between the string and the wall is θθ, as shown in the drawing. a.)  Please use the interactive area below to draw the Free Body Diagram for the small sphere. (I know the diagram isn't available this way but maybe a drawing?) b.) Enter an expression for the sum of the horizontal components of the forces in the diagram in terms of the variables given in the problem statement and standard physical constants.  c.) Enter an expression for the sum of the vertical components of the forces in the diagram in terms of the variables given in the problem statement and standard physical constants.

icon
Related questions
Question

Very lost here. Not sure where to even begin. 

 

A small sphere with mass mm and charge qq is attached to one end of a string with length LL and tension FTFT. The other end of the string is attached to a wall which has surface-charge density σσ. The angle between the string and the wall is θθ, as shown in the drawing.

a.)  Please use the interactive area below to draw the Free Body Diagram for the small sphere. (I know the diagram isn't available this way but maybe a drawing?)

b.) Enter an expression for the sum of the horizontal components of the forces in the diagram in terms of the variables given in the problem statement and standard physical constants. 

c.) Enter an expression for the sum of the vertical components of the forces in the diagram in terms of the variables given in the problem statement and standard physical constants. 

d.) Using the same values, L=L=9 cm, q=q=89 nC, σ=σ=3.4μC/m2μC/m2 and m=m=3.8 g, enter a numeric value for the tension in the string, FTFT, in newtons. 

e.) Using the same values, L=L=9 cm, q=q=89 nC, σ=σ=3.4μC/m2μC/m2 and m=m=3.8 g, enter a numeric value for the tension in the string, FTFT, in newtons. 

Add Force + + S Reset All Fg 135 x Fg + + + + + + Ftotal,x: - (neg) Ftotal,y: + (pos) + + +
Transcribed Image Text:Add Force + + S Reset All Fg 135 x Fg + + + + + + Ftotal,x: - (neg) Ftotal,y: + (pos) + + +
Expert Solution
Step 1

Given,

mass of the sphere is m

charge of the sphere is q

The length of the string is L

The surface charge density of the wall is σ

The angle between string and wall is θ

And the tension in the string is T

 

a)

Then, the free body diagram for this

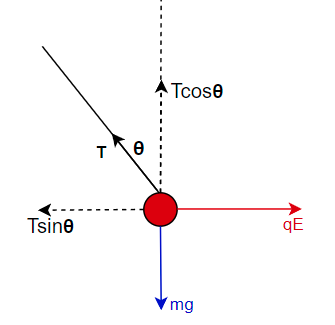
Advanced Physics homework question answer, step 1, image 1

where E is the electric field on the charged sphere due to wall

 

 

trending now

Trending now

This is a popular solution!

steps

Step by step

Solved in 3 steps with 3 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer