Question
thumb_up100%
The answer for question a
Transcribed Image Text:17:56 1
www.bartleby.com
= bartleby
Q&A
Science / Physics / Pl / A single bead can slide with negligible...
: A single bead can slide with negligibl...
Homework solutions you need when you
->
need them. Subscribe now.
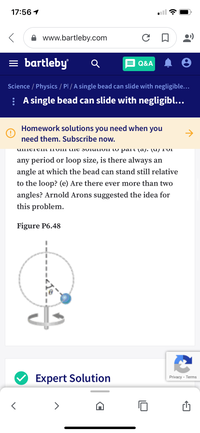
UIMCIEIIT ITOIII UIIE SOIULIOII TO palT (aj. (u) T'oI
any period or loop size, is there always an
angle at which the bead can stand still relative
to the loop? (e) Are there ever more than two
angles? Arnold Arons suggested the idea for
this problem.
Figure P6.48
Expert Solution
Privacy - Terms
<>

Transcribed Image Text:17:56 1
www.bartleby.com
= bartleby
Q&A
Science / Physics / Pl / A single bead can slide with negligible...
: A single bead can slide with negligibl...
Homework solutions you need when you
->
need them. Subscribe now.
A single bead can slide with negligible friction
on a stiff wire that has been bent into a circular
loop of radius 15.0 cm as shown in Figure
P6.48. The circle is always in a vertical plane
and rotates steadily about its vertical diameter
with a period of 0.450 s. The position of the
bead is described by the angle 0 that the radial
line, from the center of the loop to the bead,
makes with the vertical. (a) At what angle up
from the bottom of the circle can the bead slay
motionless relative to the turning circle? (b)
What If? Repeat the problem, this time taking
the period of the circle's rotation as 0.850 s. (c)
Describe how the solution to part (b) is
different from the solution to part (a). (d) For
any period or loop size, is there always an
angle at which the bead can stand still relative
to the loop? (e) Are there ever more than tv
angles? Arnold Arons suggested the idea fo
this problem.
Privacy - Terms
>
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 4 steps with 1 images

Knowledge Booster
Similar questions
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios