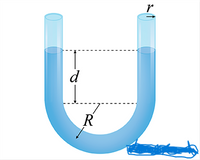
A section of uniform pipe is bent into an upright U shape and partially filled with water, which can then oscillate back and forth in simple harmonic motion. The inner radius of the pipe is r = 0.024 m. The radius of curvature of the curved part of the U is R = 0.23 m. When the water is not oscillating, the depth of the water in the straight sections is d = 0.37 m. Enter an expression for the mass of water in the tube, in terms of the defined quantities and the density of water, ρ. Use the approximation r << R.  Calculate the mass of the water, in kilograms. Take ρ = 1000 kg/m3.   Enter an expression for the force constant of the U-shaped column of water when displaced from equilibrium, in terms of the defined quantities, ρ, and g. This constant is analogous to the spring constant in Hooke’s law.   Find the value of the force constant, in newtons per meter. Take ρ = 1000 kg/m3 and g = 9.81 m/s2.  Calculate the period of oscillation, in seconds.

and w2 and Two parallel traveling plane waves have different angular frequencies @1 pressure amplitudes P₁ and P₂. (a) Show that the instantaneous energy density %; at a point in space varies between (P₁ + P₂)² / poc² and (P₁ – P₂)² / poc². (b) Show that the total energy density & at the point averages to the sum of the individual energy densities of each wave alone. Hint: Let the averaging time be much greater than 2πT/|w1 - w₂|.

Problem Consider a cylindrical pipe of length L and diameter D = 2R. The angle that the axis of the pipe forms with the vertical direction is a. Assume that when the fluid enters the pipe its velocity is uniform (i.e., it has the same value over the entire cross-section of the pipe) and equal to U in the axial direction. In the radial and angular directions, the velocity is zero. So, it is: 2 =0: v(r, 0, 2) = Ue, (1.1) Here v is the fluid velocity and e, is a vector of unit magnitude parallel to the coordinate axis z; furthermore, we have assumed that the pipe inlet is located at z = 0. Near the entrance of the pipe, the velocity profile varies in the axial direction. But after a certain entrance length, the profile becomes fully developed, no longer changing with z. The evolution of the velocity profile is sketched in Fig. 1, where, for clarity, the pipe inclination is not shown. The entrance length is denoted by L.. For z > L., the fluid velocity is no longer a function of the axial…

A sample is subjected to a hydraulic gradient of dhlax = 01 cm/cm in the x clirection and a flux qy of 0.001 cm/s in the y direction in response to this gradient (there is no gradient in the y direction). The same sample is then subjected to a hydraulic gradient of @hidy = 0.01 cm/cm in the y direction and a flux qx is measured in the x direction in response to this gradient (there is no gradient in the x direction). What is the magnitude of the flux qx in response to @hdy!