Related questions
Question
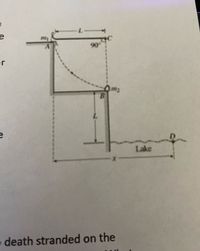
A rope of length L = 1.2 m is attached to a support at point C. A person of mass 100 kg sits on a ledge at position A holding the other end of the rope so that it is horizontal and taut, as shown. The person then drops off the ledge and swings down on the rope toward position B on a lower ledge where an object of mass 63 kg is at rest. At position B the person grabs hold of the object and simultaneously lets go of the rope. The person and the object then land together in the lake at point D, which is a vertical distance L below position B. Air resistance and the mass of the rope are negligible. Determine the total horizontal displacement x of the person from position A until the person and object land in the water at point D.
Transcribed Image Text:The image illustrates a physics problem involving a projectile and its motion. Below is a detailed description:
1. **Diagram Overview:**
- The diagram shows two masses, \( m_1 \) and \( m_2 \), involved in a system where \( m_1 \) is at point A at the edge of a horizontal surface, and \( m_2 \) is positioned at point B on a vertical surface.
- A dotted line between A and C indicates a curved trajectory, which is part of a typical projectile motion from point A to C.
- A vertical line from C to B is labeled with a right angle, denoting a perpendicular relation to the horizontal.
2. **Labeling and Measurements:**
- \( m_1 \) is positioned at point A along the horizontal section extending horizontally to point C. The horizontal distance between A and C is labeled \( L \).
- \( m_2 \) is at point B, located directly below C, with a vertical distance also marked as \( L \).
- The endpoint of the vertical drop from B is connected to the surface of a lake.
- Horizontal distance from point B along the lake is extended and marked as "Lake" towards point D.
3. **Additional Elements:**
- The configuration implies \( m_1 \) is initially moving horizontally and then follows a projectile-like path.
- The entire setup might be part of a classical mechanics problem possibly dealing with energy conservation, projectile motion, or kinematics.
This diagram helps explain relationships between different physical quantities in a typical projectile problem scenario on an educational platform.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps
Knowledge Booster
Similar questions
- The drawing shows a human figure approximately in a sitting position. For the purposes of this problem, there are three parts to the figure, and the center of mass of each one is shown in the drawing. These parts are: (1) the torso, neck, and head (total mass = 42.0 kg) with a center of mass located on the y axis at a point 0.355 m above the origin, (2) the upper legs (mass = 19.5 kg) with a center of mass located on the x axis at a point 0.178 m to the right of the origin, and (3) the lower legs and feet (total mass = 10.5 kg) with a center of mass located 0.487 to the right of and 0.206 m below the origin. Find the (a) x coordinate and (b) the y coordinate of the center of mass of the human figure. Note that the mass of the arms and hands (approximately 12% of the whole-body mass) has been ignored to simplify the drawing. (a) Number (b) Number Units Unitsarrow_forwardA meter stick is hanging from the ceiling at the 50 cm marker, perfectly in balance.. A 10 kg mass is tied to the meter stick at the 70 cm marker. A 10 kg mass is tied to the meter stick at the 80 cm marker. Where should a 20 kg mass be placed to maintain equilibrium? 25 cm 10 cm 20 cm 35 cmarrow_forwardObjects with a uniform mass distribution and a symmetric shape have a center of mass at the center of the object. For non-uniform objects, the center of mass needs to be determined experimentally. To measure the center of mass of such an object, a pivot is placed in the middle of a board and the top of the non-uniform object is placed to the right of the pivot. When a uniform 10.0 kg mass has its center placed 60.0 cm to the left of the pivot the system balances perfectly (as shown below). The mass of the non-uniform object is measured with an electronic scale in the lab and found to beM = 39.8 kg . Top of non-uniform object 10.0 kg M 60.0 cm Part A Where is the center of mass of the non-uniform object? (report the location from the top of the object, and in cm) ΑΣΦ ? dCM = стarrow_forward
- Students work together during an experiment about Newton’s laws. The students use a setup that consists of a cart of known mass connected to one end of a string that is looped over a pulley of negligible friction, with its other end connected to a hanging mass. The cart is initially at rest on a horizontal surface and rolls without slipping when released. The inertia of the cart's wheels is negligible. Students have access to common laboratory equipment to make measurements of components of the system. By collecting the appropriate data, the students can determine the relationship between the acceleration of the cart and the net force exerted on the cart. Which of the following graphs should the students produce to show the correct relationship? a A b C c D d Barrow_forwardA woman with mass m is standing on a platform and holding onto a light rope attached to a hook in the ceiling. A second rope, also attached to the hook, is being held by a man with larger mass M on a second platform. The ropes are the same length, and the ropes are initially horizontal. The two people start from rest and swing toward each other. They meet at the lowest point of their swings, and grab onto one another, swinging upward until the ropes make an angle of 32.1° with the vertical. Find the value of the ratio m/M.arrow_forwardThree ice skaters meet at the center of a rink and each stands at rest facing the center, within arm's reach of the other two. On a signal, each skater pushes himself away from the other two across the frictionless ice. After the push, skater A with mass mA = 85.0 kg moves in the negative y-direction at 3.00 m/s and skater B with mass mB = 95.0 kg moves in the negative x-direction at 4.00 m/s. Find the x- and y-components of the 90.0 kg skater C's velocity (in m/s) after the push. vCx = vCy =arrow_forward
arrow_back_ios
arrow_forward_ios