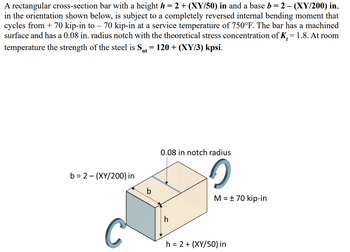
A rectangular cross-section bar with a height h = 2 + (XY/50) in and a base b = 2 - (XY/200) in, in the orientation shown below, is subject to a completely reversed internal bending moment that cycles from + 70 kip-in to 70 kip-in at a service temperature of 750°F. The bar has a machined surface and has a 0.08 in. radius notch with the theoretical stress concentration of K, = 1.8. At room - temperature the strength of the steel is S₁t = 120 + (XY/3) kpsi. ut b=2(XY/200) in b 0.08 in notch radius h C M = ± 70 kip-in h=2+(XY/50) in a) With a 90% reliability estimate, the endurance strength of the part is at a temperature of 750°F. Hint: This is a rectangular cross-section in non-rotating bending. b) What is the fatigue strength of this part if it is to survive N = (55 + XY) * 10³ cycles at 750°F?

A thin-walled hollow tube AB of conical shape has constant thickness I and average diameters dAand dBat the ends (see figure). Determine the strain energy U oT the tube when it is subjected to pure torsion by torques T, Determine the angle of twist of the tube. Note: Use the approximate formula / ird^tlA for a thin circular ring; see Case 22 of Appendix E.

Solve the preceding problem for the following data: diameter LO m, thickness 48 mm, pressure 22 MPa, modulus 210 GPa. and Poisson's ratio 0.29

A long, thin-walled tapered tube AB with a circular cross section (see figure) is subjected to a torque T. The tube has length L and constant wall thickness t. The diameter to the median lines of the cross sections at the ends A and B are dAand dB, respectively. Derive the following formula for the angle of twist of the tube: Hint: If the angle of taper is small, you may obtain approximate results by applying the formulas for a thin-walled prismatic tube to a differential element of the tapered tube and then integrating along the axis of the tube.

Two steel tubes are joined at B by four pins (dp= 11 mm), as shown in the cross section a—a in the fiaure. The outer diameters of the tubes are dAB= 41 mm and dBC= 28 mm. The wall thickness are tAB= 6.5 mm and tBC= 7.5 mm. The yield stress in tension for the steel is sy = 200 MPa and the ultimate stress in tension is ??U:= 340 MPa. The corresponding yield and ultimate values in shear for the pm are 80 MPa and 140 MPa, respectively. Finally, the yield and ultimate values in bearing R between the pins and the tubes are 260 MPa, and 450 MPa, respectively. Assume that the factors safety with respect to yield stress and ultimate stress are 3.5 and 4.5. respectively. (a) Calculate the allowable tensile force P allowconsidering tension in the tube (b) Recompute P allowfor shear in the pins.(c)Finaly, recomputed Pallowfor bearing between the pm and the tubes. Which is the tubes. Which is the controlling value value of P?

A uniformly tapered aluminum-ally tube AB of circular cross section and length L is fixed against rotation at A and B, as shown in the figure. The outside diameters at the ends are dAand dA.A hollow section of lenth L/2 and constant thickness t = dA/10 is cast into the tube and extends from B half-way toward A. Torque T0is applied at L/2. (a) Find the reactive torques at the supports, TA and TB. Use numerical values as follows: dA = 2.5 in., L = 48., G = 309 × 106 psi, and T0= 40,000 in.-lb. (b) Repeat part (a) if the hollow sections has constant diameter dA.

A solid circular bar of diameter d = 50 mm (see figure) is twisted in a testing maching until the applied torque reaches the value T = 500 N ·. At this value of torque, a strain gage oriented at 45º to the axis of the bar gives a reading e = 339 × 10-6. What is the shear modulus G of the material?

A thin-walled circular tube and a solid circular bar of the same material (see figure) are subjected to torsion. The tube and bar have the same cross-sectional area and the same length. What is the ratio of the strain energy U1in the tube to the strain energy U2in the solid bar if the maximum shear stresses are the same in both cases? (For the tube, use the approximate theory for thin-walled bars.)

An aluminum tube has inside diameter dx= 50 mm, shear modulus of elasticity G = 27 GPa, v = 0.33, and torque T = 4.0 kN · m. The allowable shear stress in the aluminum is 50 MPa, and the allowable normal strain is 900 X 10-6. Determine the required outside diameter d2 Re-compute the required outside diameter d2, if allowable normal stress is 62 MPa and allowable shear strain is 1.7 X 10-3.

A solid circular bar of steel (G = 1L4 × 106 psi) with length L = 30 in, and diameter d = 1.75 in, is subjected to pure torsion by torques T acting at the ends (see figure). Calculate the amount of strain energy V stored in the bar when the maximum shear stress is 4500 psi. From the strain energy, calculate the angle of twist 0 (in degrees).