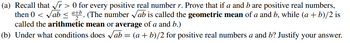
(a) Recall that √√r> 0 for every positive real number r. Prove that if a and b are positive real numbers, then 0 <√ab atb. (The number √ab is called the geometric mean of a and b, while (a + b)/2 is ≤ called the arithmetic mean or average of a and b.) (b) Under what conditions does √ab = (a + b)/2 for positive real numbers a and b? Justify your answer.

You forgot to solve the other question. The other question is 'Restate definition 4 in your own words as you understand it.'

In 2004 it surfaced in Reader's Digest presented as having happened to a teacher at an unnamed community college. Four students walked in halfway through American history test my father was giving at the local community college. "Sorry," they said, "we had a flat tire." An understanding man, Dad said that if they could answer just one question correctly, he would give them each an "A" for the exam. The students agreed. So my father handed each one a piece of paper, placed them in four separate comers and said, "Write down which tire was flat." Kurt Smith What is the probability that these four students would give identical answers if they hadn't had a flat tire? Why?

can you please explain further what is being said I do not understand