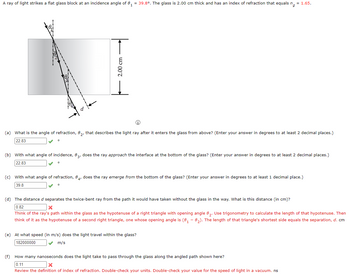
A ray of light strikes a flat glass block at an incidence angle of 8₁ = 39.8°. The glass is 2.00 cm thick and has an index of refraction that equals no = 1.65. 2.00 cm (a) What is the angle of refraction, 82, that describes the light ray after it enters the glass from above? (Enter your answer in degrees to at least 2 decimal places.) 22.83 (b) with what angle of incidence, 83, does the ray approach the interface at the bottom of the glass? (Enter your answer in degrees to at least 2 decimal places.) 22.83 (c) with what angle of refraction, 84, does the ray emerge from the bottom of the glass? (Enter your answer in degrees to at least 1 decimal place.) 39.8 O (d) The distance d separates the twice-bent ray from the path it would have taken without the glass in the way. What is this distance (in cm)? 0.82 x Think of the ray's path within the glass as the hypotenuse of a right triangle with opening angle 82. Use trigonometry to calculate the length of that hypotenuse. The think of it as the hypotenuse of a second right triangle, one whose opening angle is (0₁-0₂). The length of that triangle's shortest side equals the separation, d. cn (e) At what speed (in m/s) does the light travel within the glass? 182000000 m/s (f) How many nanoseconds does the light take to pass through the glass along the angled path shown here? X 0.11 Davis

Refraction is a change in the direction of light rays when they travel from one medium to another. It is the bending of light when it goes through different media.

Light is considered by many scientists to have dual nature, both particle nature and wave nature. First, Particle nature is one in which we consider a stream of packets of energy called photons. Second, Wave nature is considering light as electromagnetic…

Diamond, the world’s hardest naturally occurring material and mineral known, is a solid form of the element carbon. The atoms are arranged in a crystal structure called diamond cubic. They exist in a huge variety of colours. Also, they are one of the bes…