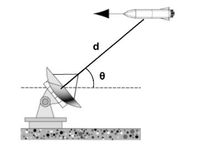
A radar station detects an incoming missile. At first contact, the missile is found to be a distance d = 57.5 miles away from the radar dish, at an angle of θ = 30.0 ̊ from the horizon. After 2.50 seconds, the missile is detected a distance d = 17.5 miles away from the radar dish, at an angle of θ = 70.0 ̊ from the horizon. (a) Calculate the average velocity of the missile during this time in Cartesian form (x and y components). Use a coordinate system where the +x direction is to the right, the +y direction is up, and the origin is at the location of the satellite dish.

During the battle of Bunker Hill, Colonel William Prescott ordered the American Army to bombard the British Army camped near Boston. The projectiles had an initial velocity of 43 m/s at 33° above the horizon and an initial position that was 36 m higher than where they hit the ground. How far did the projectiles move horizontally before they hit the ground? Ignore air resistance.

A plane flies 493 km east from city A to city B in 45.0 min and then 983 km south from city B to city C in 1.30 h. For the total trip, what are the (a) magnitude and (b) direction of the plane's displacement, the (c) magnitude and (d) direction of its average velocity, and (e) its average speed? Give your angles as positive or negative values of magnitude less than 180 degrees, measured from the +x direction (east). (a) Number i Units (b) Number Units (c) Number i Units (d) Number i Units (e) Number Units II

A ball thrown horizontally at vi = 25.0 m/s travels a horizontal distance of d = 50.0 m before hitting the ground. From what height h was the ball thrown?

Questions 1 through 3 pertain to the situation described below: An archer wants to launch an arrow from a bow to clear a treetop that is 35.0 m vertically above, and 97.0 m horizontally away from, the launching location. Assume that the launching speed is 57.0 m/s and the launching angle is 0 above the horizontal. (1) How much does the arrow clear the treetop if 0 = 30.0°? (A) 3.6 m; (B) 3.1 m; (C) 2.6 m; (D) 2.1 m; (E) 1.6 m. (2) What is the maximum horizontal range of the arrow if 0 can vary? (A) 212 m; (B) 242 m; (C) 272 m; (D) 302 m; (E) 332 m. (3) What is the range of 0 for the arrow to clear the treetop? (A) 29.9-86.0°; (B) 28.9–81.0°; (C) 27.9–76.0°; (D) 26.9–71.0°; (E) 25.9–66.0°.

An object has an initial velocity of 29.0 m/s at 95.0° and an acceleration of 1.90 m/s2 at 200.0°. Assume that all angles are measured with respect to the positive x-axis. (a) Write the initial velocity vector and the acceleration vector in unit vector notation. (b) If the object maintains this acceleration for 12.0 seconds, determine the average velocity vector over the time interval. Express your answer in your unit vector notation.

A particle initially located at the origin has an acceleration of a = 4.00j m/s? and an initial velocity of v = 9.00î m/s. (a) Find the vector position of the particle at any time t (where t is measured in seconds). tî + 2 j) m (b) Find the velocity of the particle at any time t. î + tj) m/s (c) Find the coordinates of the particle at t = 6.00 s. y%3D m (d) Find the speed of the particle at t = 6.00 s. m/s Need Help? Read It Watch It P Type here to search

A pilot flies with a plane 20 km northward with an angle of 60 east ➚ , then 30 km to the east ⮕ , then 10 to the  north ⬆ , what is its distance from the start and what is its direction

A soccer player kicks a 550g soccer ball from the ground at sea level. The ball leaves his foot at a velocity of 25.0m/s[West 15° Up]. If the ball lands on ground which is also at sea level, what was the range of the kick?

A GPS tracking device is placed in a police dog to monitor its whereabouts relative to the police station. At time t₁ = 23 min, the dog's displacement from the station is 1.2 km, 33° north of east. At time t₂ = 57 min, the dog's displacement from the station is 2.0 km, 75° north of east. Find the magnitude and direction of the dog's average velocity between these two times. 1.4 m/s, 31° west of north 0.80 m/s, 42° west of north 1.6 m/s, 42° north of east 0.52 m/s, 88° north of east 0.67 m/s, 21° west of north