Question
A Quantum Harmonic Oscillator, with potential energy V(x) = ½ mω02x2, where m is the mass of the particle in the potential, and ω0 is a constant.
Determine the value of the quantum number n for the wavefunction provided. Explain how the result is obtained, as well as state a numerical value.
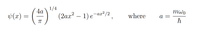
Transcribed Image Text:1/4
(3)
4а
mwo
V(x)
(2ax? – 1) e-a² /2
where
а —
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 4 steps

Knowledge Booster
Similar questions
- Consider a quantum particle with energy E approaching a potential barrier of width L and heightV0 > E from the right (as shown in image). The wavefunction of the particles in the region x > L is given by ψ = A exp {−i (kx + ωt)} , where A, k and ω are all constants. Use the Gamow factor formalism to calculate an approximate expression for the transmission rate of these particles through the barrier.arrow_forwardWe will consider the Schrödinger equation in this problem as well as the analogies between the wavefunction and how boundary conditions are an essential part of developing this equation for various problems (situations). a) Write the form of the time-independent Schrödinger equation if the potential is that of a spring with spring constant k. Write the form of the time-dependent Schrödinger equation with the same potential. Briefly describe all the terms and variables in these equations. b) One solution to the time independent Schrödinger equation has the form Asin(kx). Why might it be called the wavefunction? If this form represents a wave of light, what is the energy for one photon? (Notek here stands for the wavevector and not the spring constant.) c) Why must all wavefunctions go to zero at infinite distance from the center of the coordinate system in all systems where the potential energy is always finite?arrow_forwardThe potential energy of a harmonic oscillator is U = kx. Show that the expectation value (U) of U is E0 / 2 when the oscillator is in the state n = 0. (In fact, this is true for all states of the harmonic ocillator.) What is the expected value of the kinetic energy of the oscillator? How do these results compare to the classical values of Ū and KE ?arrow_forward
- the ground state wavefunction of a quantum mechanical simple harmonic oscillator of mass m and frequency, which is given by: Question mw where a = the potential is V(x) = mw²x² and N is given by: N =) 9 ax² ¡Ent Yo (x, t) = Ne ze By substituting into the time-dependent Schrödinger equation, prove that the ground state energy, Eo, is given by: Eo ħw 2arrow_forwardIn the lab you make a simple harmonic oscillator with a 0.15-kg mass attached to a 12-N/m spring. (a) If the oscillation amplitude is 0.10 m, what is the corresponding quantum number n for the quantum harmonic oscillator? (b) What would be the amplitude of the quantum ground state for this oscillator? (c) What is the energy of a photon emitted when this oscillator makes a transition between adjacent energy levels? Comment on each of your results.arrow_forward
arrow_back_ios
arrow_forward_ios