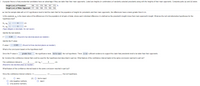
A popular theory is that presidential candidates have an advantage if they are taller than their main opponents. Listed are heights (in centimeters) of randomly selected presidents along with the heights of their main opponents. Complete parts (a) and (b) below. Height (cm) of President Height (cm) of Main Opponent 177 180 169 175 190 184 186 172 176 185 187 175 O a. Use the sample data with a 0.01 significance level to test the claim that for the population of heights for presidents and their main opponents, the differences have a mean greater than 0 cm. In this example, Hg is the mean value of the differences d for the population of all pairs of data, where each individual difference d is defined as the president's height minus their main opponent's height. What are the null and alternative hypotheses for the hypothesis test? Ho Hg = cm H: Ha> (Type integers cm decimals. Do not round.) Identify the test statistic. t= 0.28 (Round to two decimal places as needed.) Identify the P-value P.value = 0.395 (Round to three decimal places as needed.) What is the conclusion based on the hypothesis test? Since the P-value is greater than the significance level, fail to reject the null hypothesis. There is not sufficient evidence to support the claim that presidents tend to be taller than their opponents. b. Construct the confidence interval that could be used for the hypothesis test described in part (a). What feature of the confidence interval leads to the same conclusion reached in part (a)? The confidence interval is cm < Hg cm (Round to one decimal place as needed.) What feature of the confidence interval leads to the same conclusion reached in part (a)? Since the confidence interval contains (1) (2) the null hypothesis. O zero, O only negative numbers, O only positive numbers, (2) O fail to reject O reject (1)

ent/d/1aclVc5owmTUnYTxfQ40XLtNTfC97Tz96UgSvlS8pwk/ ADEMY_MATH 7_UNIT 6 WEEK 7 G Extensions Help Accessibility ext W Arial 2 Question 3 12 + BIU 1.12r+t-4r + 6t 2. (12r + 2) - (4r + 10f) 3.12(r+t) -6(r+t) − 4(r+f) − 2(r+f) 4 Match each expression in column A with an equivalent expression from column B. Show or explain your reasoning. Column A Column B • 8(r-t) 8(r+t) • Br+7t For each situation, write an expression for the new balance using as few terms as possible. Y

M Inbox - thatisdumb202 x M (no subject) - jonah.her x * gZqWqPtAcsQpUWNz- x should i side wvith the E DeltaMath b Math Homework Help, x G how do i take a screens + Process Photos: Week DeltaMath A deltamath.com/student/solve/12668563/xGameLevel3 Delta Math Student Help Video Tools - < Вack Give up Show Example Record: 0/3 Score: o Penalty: None Complete: 28% Jonah Hendon The X Game (Level 3) Feb 05, 10:14:08 AM Watch help video Write two numbers that multiply to the value on top and add to the value on bottom. -96 .4 Submit Answer Activate Windows Go to Settings to activate Windows. Privacy Policy Terms of Service Copyright © 2021 DeltaMath.com. All Rights Reserved. 10:27 AM P Type here to search 2/5/2021 22 行