
MATLAB: An Introduction with Applications
6th Edition
ISBN: 9781119256830
Author: Amos Gilat
Publisher: John Wiley & Sons Inc
expand_more
expand_more
format_list_bulleted
Question
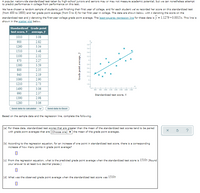
Transcribed Image Text:**Educational Website: Analysis of Standardized Test Scores and College GPA**
A popular, nationwide standardized test taken by high-school juniors and seniors may or may not measure academic potential, but it can still predict performance in college to some extent. We randomly selected students who finished their first year of college, recorded their test scores (ranging from 400 to 1600), and noted their first-year GPA (on a 0 to 4 scale).
### Data Table
The data set of standardized test scores (x) and corresponding GPAs (y) is as follows:
| Standardized test score, x | Grade point average, y |
|----------------------------|------------------------|
| 1010 | 3.08 |
| 900 | 2.32 |
| 1260 | 3.22 |
| 1000 | 2.84 |
| 1510 | 3.48 |
| 1300 | 3.12 |
| 920 | 1.96 |
| 800 | 2.35 |
| 940 | 2.19 |
| 1060 | 2.90 |
| 1210 | 2.73 |
| 1490 | 3.06 |
| 990 | 2.37 |
| 1390 | 2.98 |
| 1280 | 3.06 |
### Scatter Plot and Regression Line
The scatter plot shows the relationship between standardized test scores and GPAs. The plotted points indicate individual student data. The graph includes a least-squares regression line, \( \hat{y} = 1.1279 + 0.0015x \), suggesting a positive correlation between the test scores and GPAs.
### Analysis Questions
Based on the data and regression line:
(a) For test scores greater than the mean, the corresponding GPAs tend to be (Choose one: above/below/equal to) the mean GPA.
(b) According to the regression equation, an increase of one point in the test score corresponds to an increase in GPA by approximately 0.0015 points.
(c) To predict the GPA when the test score is 1510, use the regression equation: \( \hat{y} = 1.1279 + 0.0015(1510
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 1 images

Knowledge Booster
Similar questions
- The first test a doctor would order to determine whether a person is infected with HIV (the virus that causes AIDS) is the ELISA test. It detects antibodies and antigens for HIV. A study in Statistical Science by J. Gastwirth estimated that, if the person is actually infected with HIV, this test produces a positive result 97.7% of the time. If a person is not infected with HIV, the test result is negative 92.6% of the time. According the the US Centers for Disease Control (CDC), an estimated 1.1 million Americans out of a population of 321 million were infected with HIV in 2015. Using the information above, determine the probability that a randomly selected person whose ELISA test is positive actually is infected with HIV? a. What is the probability that a randomly selected American is infected with HIV? b. Using the answer to part (a) and the conditional probabilities of positive and negative ELISA test results, fill out the contingency table below: ELISA Test Result…arrow_forwardA statistics professor would like to build a model relating student scores on the first test to the scores on the second test. The test scores from a random sample of 21 students who have previously taken the course are given in the table. Student Test Grade 1 Test Grade 21 42 812 51 743 88 624 99 575 54 726 66 737 87 638 99 579 97 5810 89 6311 42 7712 71 6313 96 5514 56 7615 75 6916 57 7017 62 7518 89 6319 50 7220 56 7221 89 57Step 1 of 2 : Using statistical software, estimate the parameters of the modelSecond Test Grade=β0+β1(First Test Grade)+εi.Enter a negative estimate as a negative number in the regression model. Round your answers to 4 decimal places, if necessary.arrow_forwardA randomly sampled group of patients at a major U.S. regional hospital became part of a nutrition study on dietary habits. Part of the study consisted of a 50-question survey asking about types of foods consumed. Each question was scored on a scale from one (most unhealthy behavior) to five (most healthy behavior). The answers were summed and averaged. The population of interest is the patients at the regional hospital. The current survey was implemented after patients were subjected to this education, and it produced the following sample statistics for 25 patients sampled: and s = 1.02. We would like to know if the education improved nutrition behavior. We test the hypotheses H 0: = 2.9 versus Ha: > 2.9. The value of the t test is 1.96, and: a. P-value > 0.1. b. 0.025 P-value < 0.05. c. 0.25 P-value < 0.01. d. 0.05 P-value < 0.1. Given the least squares regression line y = 3 x – 3, which of the following is true? a. The…arrow_forward
- A popular, nationwide standardized test taken by high-school juniors and seniors may or may not measure academic potential, but we can nonetheless attempt to predict performance in college from performance on this test. We have chosen a random sample of students just finishing their first year of college, and for each student we've recorded her score on this standardized test (from 400 to 1600) and her grade point average (from 0 to 4) for her first year in college. The data are shown below, with x denoting the score on the standardized test and y denoting the first-year college grade point average. The least-squares regression line for these data is y = 1.1279 +0.0015x. This line is shown in the scatter plot below. Standardized Grade point test score, x average, y 1010 3.08 900 2.82 1260 3.34 3.6- 1510 3.48 3.4- 1100 2.32 3.2. 870 2.27 2.8. 1360 3.59 2.6+ 800 2.35 2.4- 940 2.19 2.2 1060 2.90 1.8. 1210 2.73 1490 3.06 800 900 1000 1100 1200 1300 1400 1500 990 2.37 Standardized test…arrow_forwardIn a study researching how donating to charity can affect a person's happiness, 96 participants were given $5 a day for one week. Each participant was randomly assigned to one of two groups. Those assigned to the first group were asked to spend the money on themselves, and those assigned to the second group were asked to donate the money to charity. At the end of the week, all of the participants were asked to rate their overall level of happiness on a scale from 0 to 100, with higher scores indicating greater levels of happiness. Which of the following are the appropriate null and alternative hypotheses to test whether the sample data provide convincing statistical evidence that donating to charity results in greater happiness than spending on oneself, on average? Ho self- "charity = 0 (A) Ha self charity >0 Ho self Mcharity=0 (B) Ha self charity 0 (E) Ha self = Mcharity <0arrow_forwardIn statistics, the data we work with is just one part of a bigger picture called the ____. In statistics, the data we work with is just one part of a bigger picture called thearrow_forward
- A randomly sampled group of patients at a major U.S. regional hospital became part of a nutrition study on dietary habits. Part of the study consisted of a 50-question survey asking about types of foods consumed. Each question was scored on a scale from one (most unhealthy behavior) to five (most healthy behavior). The answers were summed and averaged. The population of interest is the patients at the regional hospital. A prior survey of patients had found the mean score for the population of patients to be μ=2.9 After careful review of these data, the hospital nutritionist decided that patients could benefit from nutrition education. The current survey was implemented after patients were subjected to this education, and it produced the following sample statistics for the 15 patients sampled: x¯=3.5 and s=1.2 We would like to know if the education improved nutrition behavior. We test the hypotheses H0:μ=2.9 versus Ha:μ>2.9. The tt test to be used has the test statistic: Answer:arrow_forwardA popular, nationwide standardized test taken by high-school juniors and Españ seniors may or may not measure academic potential, but we can nonetheless attempt to predict performance in college from performance on this test. We have chosen a random sample of students just finishing their first year of college, and for each student we've recorded her score on this standardized test (from 400 to 1600) and her grade point average (from o to 4) for her first year in college. The data are shown below, with x denoting the score on the standardized test andy denoting the first-year college grade point average. The least-squares regression line for these data is 1.1239+0.0015x. This line is shown in the scatter plot below. Standardized test score, .x 1360 1100 790 1280 890 Grade point average, y 3.77 2.28 2.35 2.91 2.64 2.22 3.18 3.34 2.36 3.30 3.02 2.88 860 1400 1510 1000 1250 1060 1210 1020 940 1510 Send data to calculator ✓ Send data to Excel 3.07 2.29 3.01 Grade point average, 34- 324 900…arrow_forwardLynn University wants to examine whether students display better academic performance in class versus online. They have collected GPAs of two different samples of students, a sample from classes that take place in-person and a sample from classes that take place online. The data set is below. They predict that in-class students perform better than online students. GPA's In Class GPA Online GPA 4.0 4.0 3.5 2.2 3.7 3.3 3.5 3.7 2.0 2.5 3.2 3.8 3.3 3.8 What type of t-test should we use for this research question? Group of answer choices a) One sample b) Independent samples c) Paired Samplesarrow_forward
- I only need help with the last 2 pleasearrow_forwardA researcher is interested in the relationship between age and golf performance. The researcher claims that golf performance improves with age, that is, as one gets older, his or her golf scores decrease. [In golf, a low score represents better performance; a higher score represents worse performance.] The researcher randomly selects a group of eight golfers at the local golf course and records their ages and their most recent golf score. The data that were collected are presented below: Golfer's Name Diego Tiger Bogart Marilyn Jennifer Mitch Bubba Amber Age (years) Variable 1 23 14 38 43 49 36 72 Golf Score Variable 2 92 112 77 84 81 72 79 86 Which of the following are the correct statements of the null and alternate hypotheses, Ho and HA? O Ho: M₁ M₂ and HA: H1 H₂arrow_forwardDo people feel hungrier after sampling a healthy snack? Researchers randomly assign volunteers into one of three groups. The people in the first group were asked to taste a snack that was billed as a new health bar containing high levels of protein, vitamins, and fiber. The people in the second group were asked to taste the same snack but there told it was a tasty chocolate bar with a raspberry center. After tasting the snack, participants were asked to rate their hunger on a scale from 1 (not at all hungy) to 7 (very hungry). The people in the third group were asked to rate their hunger but were not given a snack. Healthy Tasty No Snack 8 3 3 7 1 3 7 3 5 4 2 6 5 6 5 a. Perform a complete one-way ANOVA hypothesis test. Test at the .05 level of significance.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman

MATLAB: An Introduction with Applications
Statistics
ISBN:9781119256830
Author:Amos Gilat
Publisher:John Wiley & Sons Inc

Probability and Statistics for Engineering and th...
Statistics
ISBN:9781305251809
Author:Jay L. Devore
Publisher:Cengage Learning

Statistics for The Behavioral Sciences (MindTap C...
Statistics
ISBN:9781305504912
Author:Frederick J Gravetter, Larry B. Wallnau
Publisher:Cengage Learning

Elementary Statistics: Picturing the World (7th E...
Statistics
ISBN:9780134683416
Author:Ron Larson, Betsy Farber
Publisher:PEARSON

The Basic Practice of Statistics
Statistics
ISBN:9781319042578
Author:David S. Moore, William I. Notz, Michael A. Fligner
Publisher:W. H. Freeman

Introduction to the Practice of Statistics
Statistics
ISBN:9781319013387
Author:David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:W. H. Freeman