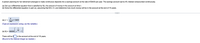
A person planning for her retirement arranges to make continuous deposits into a savings account at the rate of $3400 per year. The savings account earns 4% interest compounded continuously.(a) Set up a differential equation that is satisfied by f(t), the amount of money in the account at time t.(b) Solve the differential equation in part (a), assuming that f(0) = 0, and determine how much money will be in the account at the end of 16 years.4(a) y' =-y+ 3400100%3D(Type an expression using y as the variable.)t(b) f(t) = 8500025- 1There will be $in the account at the end of 16 years.(Round to the nearest integer as needed.)

Introduction: A differential equation is an equation that contains the derivative of an unknown…

Answered: A person planning for her retirement…

Advanced Engineering Mathematics

10th Edition

ISBN:9780470458365

Author:Erwin Kreyszig

Publisher:Erwin Kreyszig

Chapter2: Second-order Linear Odes

Section: Chapter Questions

Problem 1RQ

See similar textbooks

Similar questions

dP dt =rP-ap² Think of a small population of fish growing in a public pond - P measures the number of fish and t measures the number of years since the pond was stocked. P' = 2P 0.01P² to allow harvesting of 75 fish per year, adapt the logistic model to handle this. That is, write a differential equation based on the logistic model that incorporates the idea of harvesting 75 fish per year. [Hint: (total rate) = (rate in) - (rate out) ]
A fish hatchery has 500 fish at time ? = 0. Each year 40 fish are harvested (evenly, throughoutthe year). The population’s instantaneous growth rate is 10% per year. Thus after 1 year, if nofish were harvested, there would be slightly more than 550 fish. a) Create the modeling differential equation for the amount of the number of fish in the hatchery, y, at time t.b) Solve the differential equation.c) Is there a steady-state level of the number of fish in the hatchery?
A virus has already infected 4 million people in a country before a vaccine becomes available to the public. Once vaccination starts, the number of infected people decreases at a rate that is proportional to the cube of the number of infected people. One month later, there are still 2 million people that are infected. Let p be the number of infected people (in millions) and t be the number of months since vaccination has started. (a) Find a differential equation and initial conditions to model the situation. (b) Solve the differential equation to find pp as a function of t (c) How many people are still infected three months after vaccination starts?
In 30 min
Asap
Write a differential equation to model this physical situation. Snow is falling at a constant rate of 3/5 in per hour. It is being removed at a constant rate of 45% of the amount of snow on the ground per hour. If we use h(t) as the height of the snow at time t, and the removal of snow began at a height of 4 in --such that h(0)=4 --what would be the equation for the rate of change of the height as a function of time?
Please explain how to solve, thank you!
A loan account accrues interest at a rate proportional to its value. Suppose thatthis interest is compounded continuously in time at interest rate r, and supposethat payments of p dollars per year are made in a way that can be consideredto be continuous in time. write the differential equation and solve

Recommended textbooks for you

Advanced Engineering Mathematics

Advanced Math

ISBN:

9780470458365

Author:

Erwin Kreyszig

Publisher:

Wiley, John & Sons, Incorporated

Numerical Methods for Engineers

Advanced Math

ISBN:

9780073397924

Author:

Steven C. Chapra Dr., Raymond P. Canale

Publisher:

McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…

Advanced Math

ISBN:

9781118141809

Author:

Nathan Klingbeil

Publisher:

WILEY

Advanced Engineering Mathematics

Advanced Math

ISBN:

9780470458365

Author:

Erwin Kreyszig

Publisher:

Wiley, John & Sons, Incorporated

Numerical Methods for Engineers

Advanced Math

ISBN:

9780073397924

Author:

Steven C. Chapra Dr., Raymond P. Canale

Publisher:

McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…

Advanced Math

ISBN:

9781118141809

Author:

Nathan Klingbeil

Publisher:

WILEY

Mathematics For Machine Technology

Advanced Math

ISBN:

9781337798310

Author:

Peterson, John.

Publisher:

Cengage Learning,

Basic Technical Mathematics

Advanced Math

ISBN:

9780134437705

Author:

Washington

Publisher:

PEARSON

Topology

Advanced Math

ISBN:

9780134689517

Author:

Munkres, James R.

Publisher:

Pearson,

SEE MORE TEXTBOOKS