Question
A pendulum of length L and mass M has two (2) identical springs connected to it as shown. Assume the same constant k for both springs. Find the frequency of vibration of the system for small values of the amplitude (small θ). Assume the vertical suspension rod of length L is rigid, but ignore its mass.
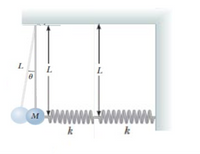
Transcribed Image Text:L.
L
L.
M WWWW-wwww
k
k
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps

Knowledge Booster
Similar questions
- A 2-kg mass is attached to a spring with stiffness 56 N/m. The damping constant for the system is 8√√7 N-sec/m. If the mass is pulled 10 cm to the right of equilibrium and given an initial rightward velocity of 4 m/sec, what is the maximum displacement from equilibrium that it will attain?arrow_forwardThe length of a simple pendulum is 0.85 m and the mass of the particle (the "bob") at the end of the cable is 0.28 kg. The pendulum is pulled away from its equilibrium position by an angle of 6.9° and released from rest. Assume that friction can be neglected and that the resulting oscillatory motion is simple harmonic motion. (a) What is the angular frequency of the motion? (b) Using the position of the bob at its lowest point as the reference level, determine the total mechanical energy of the pendulum as it swings back and forth. (c) What is the bob's speed as it passes through the lowest point of the swing? O 0arrow_forwardA 3-kg mass is attached to a spring with stiffness 60 N/m. The damping constant for the system is 12√5 N-sec/m. If the mass is pulled 20 cm to the right of equilibrium and given an initial rightward velocity of 4 m/sec, what is the maximum displacement from equilibrium that it will attain?arrow_forward
- A simple pendulum has a mass of 0.450 kg and a length of 5.00 m. It is displaced through an angle of 13.0° and then released. Using the analysis model of a particle in simple harmonic motion, calculate the following. (Give your answer to the thousandths place.) (b) What is the maximum angular acceleration of the bob?arrow_forwardA mathematical pendulum swings with angular amplitude α (α ≪ 1), its period is T . By what factor does the period of the pendulum change if it is suddenly surrounded by two perfectly elastic walls (see figure)? The walls are arranged symmetrically, their angular distance is α.arrow_forwardYou have made a physical pendulum by swinging a rod of mass M = 1.08 kg and length L = 1.45 meters around its end. The mass of the rod is distributed uniformly along its length. We will assume that the amplitude of the swing is max = 19.34 degrees. Solid Rod Swings in Simple Harmonic Motion ^ 0=-0, max 0=+0₁ max Determine all the following: The FORMULA for the moment of inertia of your rod, I = The distance from the pivot point to the Center-Of-Mass, d = The angular frequency of the pendulum, w = The amplitude of the motion in radians, max = radians The angular velocity when 0 = 64% of full swing, w(0 = 0.64 0max): NOTE: The first question requires a FORMULA, not a value. rad/sec = meters rad/secarrow_forward
- The suspension system of a 2200 kg car is made of springs that are compresses by 8 cm when the mass of the car is placed on it. Also, the collision amplitude decreases by 50% each cycle. Find the damping constant 6 (in units of kg/s) for the spring and shock absorber system of one wheel, assuming each wheel supports 550 kg. 134arrow_forwardThe length of a simple pendulum is 0.75 m and the mass of the particle (the "bob") at the end of the cable is 0.39 kg. The pendulum is pulled away from its equilibrium position by an angle of 8.9° and released from rest. Assume that friction can be neglected and that the resulting oscillatory motion is simple harmonic motion. (a) What is the angular frequency of the motion? (b) Using the position of the bob at its lowest point as the reference level, determine the total mechanical energy of the pendulum as it swings back and forth. (c) What is the bob's speed as it passes through the lowest point of the swing? (a) Number i 0.58 Units rad/s (b) Number i 0.037 Units (c) Number i 0.435 Units m/sarrow_forwardThe torsional spring of constant kt = 58 N-m/rad is undeformed when 0 = 0. Determine the value(s) of 0 over the range 0 ≤ 0 ≤ 180° for which equilibrium exists. Use the values mA = 12 kg, mB = 1 kg, moA = 7 kg, and r = 0.9 m. Assume that OA is a uniform slender rod with a particle A (negligible size) at its end, and neglect the effects of the small ideal rollers. You should find two answers, 0₁ <0₂. mB B Answers: KTI i o( 0₁ = 0₂= i 151.5 34.5 A MOA MAarrow_forward
arrow_back_ios
arrow_forward_ios