
MATLAB: An Introduction with Applications
6th Edition
ISBN: 9781119256830
Author: Amos Gilat
Publisher: John Wiley & Sons Inc
expand_more
expand_more
format_list_bulleted
Question
Can you use the Rstudio to calculate some value please. Thank you!

Transcribed Image Text:A particular coin is biased. Each time it is flipped, the probability of a head is P (H) = 0.95 and the probability of a
tail is P(T) = 0.05. Each flip is independent of the other flips. The coin is flipped twice. Let X be the total number of
times the coin shows a head out of two flips. So the possible values of X are x = = 0, 1, or 2.
a) How would we find P(X=2) ? (Pick all right answers)
Type in Rstudio: choose(1, 1)* 0.95^0 * 0.05^2
✔ Type in Rstudio: choose(2, 2)* 0.95^2 * 0.05^0
□ P(X = 2) = (²) P(H)² (1 – P(H))²—2
○ P(X = 2) = (²)P(H)¹ (1 — P(H))²–1
Knowing that P(X = 1) = 0.095 and P(X= 2) = 0.9025 , compute the following probabilities:
P(X=0)
= 0.0025
(Enter the exact value)
b) What is the probability that X ≥ 1?
0.0025
(Enter the exact value)
c) Compute the expected value of X.
"X=
d) Compute the variance X.
0²=
=
(Enter the exact value)
(Enter the exact value)
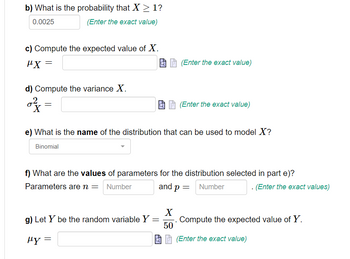
Transcribed Image Text:b) What is the probability that X ≥ 1?
0.0025
(Enter the exact value)
c) Compute the expected value of X.
μ.Χ
d) Compute the variance X.
of
=
(Enter the exact value)
e) What is the name of the distribution that can be used to model X?
Binomial
g) Let Y be the random variable Y =
μy =
(Enter the exact value)
f) What are the values of parameters for the distribution selected in part e)?
Parameters are n = Number
and p = Number
X
50
. (Enter the exact values)
Compute the expected value of Y.
(Enter the exact value)
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 5 steps

Knowledge Booster
Similar questions
- this is incorrect and due at 5:00 please helparrow_forwardHello Please help me make the correct decimal placement for 0.9854 if it is necessary to round to three decimal places as needed. Thank you for your time. Genearrow_forwardOnly need help with 1 & 2. Must be calculated in Excel. Thanksarrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman

MATLAB: An Introduction with Applications
Statistics
ISBN:9781119256830
Author:Amos Gilat
Publisher:John Wiley & Sons Inc

Probability and Statistics for Engineering and th...
Statistics
ISBN:9781305251809
Author:Jay L. Devore
Publisher:Cengage Learning

Statistics for The Behavioral Sciences (MindTap C...
Statistics
ISBN:9781305504912
Author:Frederick J Gravetter, Larry B. Wallnau
Publisher:Cengage Learning

Elementary Statistics: Picturing the World (7th E...
Statistics
ISBN:9780134683416
Author:Ron Larson, Betsy Farber
Publisher:PEARSON

The Basic Practice of Statistics
Statistics
ISBN:9781319042578
Author:David S. Moore, William I. Notz, Michael A. Fligner
Publisher:W. H. Freeman

Introduction to the Practice of Statistics
Statistics
ISBN:9781319013387
Author:David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:W. H. Freeman