Question
A particle with a mass m and a kinetic energy E > 0 approaches an abrupt potential drop Vo. What is the propability that it will be reflected back if E = 4Vo/3?
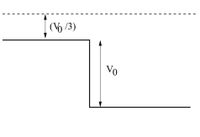
Transcribed Image Text:(V /3)
Vo
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 1 images

Knowledge Booster
Similar questions
- A particle is confined in a box of length L. The momentum is quantized and we find that the lowest possible value of the momentum for a particle in that box is 1.3 E-24 kg.m2/s. What is the length of the box? Express your answer in Angstroms (1E-10 m)arrow_forwardIf density of mercury is 13600 kg/ m = 9.8 m/s?. Find the energy of translation 3 and g %3D per cubic metre of oxygen at N.T.P.arrow_forwardCalculate the de Broglie wavelength (in fm) of a 5.8 MeV a particle emitted from an atomic nucleus whose diameter is approximately 1.6 × 10¯14, fm Calculate its minimum kinetic energy (in keV) according to the uncertainty principle. keV Could this particle exist inside the nucleus? Yes No Explain. m.arrow_forward
- Problem 9: Rutherford Scattering A gold foil (5.9×1022 atoms/cm³) of "hair" thickness 80 µm is used in a Rutherford experiment to scatter a particles with energy 5 MeV. Find the fraction of particles scattered at angles 0 > 30°.arrow_forwardElectrons are fired at a rectangular potential energy barrier, once every 149 ms. If the barrier is 2.55 nm thick and has a height that exceeds the energy of the incident electrons by exactly 712 meV, how long on average would you expect to wait for one electron to pass through the barrier? 8.57 x105 average wait: Incorrectarrow_forwardThe electron moves in an infinitely deep. potential well with a width of l=0.15 nm. a) Calculate the minimum (i.e. ground state) speed of the electron. V₁=? b) Calculate the reaction force that the electron causes when it moves back and forth and collides with the other wall of the well adiabatically (thermally insulated). F=? c) Calculate the frequency of the electron's back and forth motion. f=?arrow_forward
arrow_back_ios
arrow_forward_ios