Question
fast plss
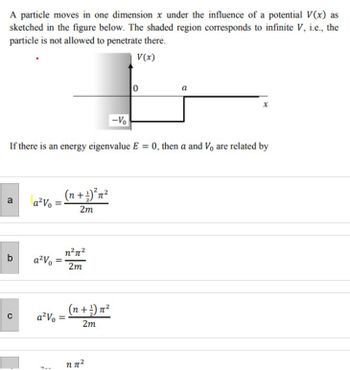
Transcribed Image Text:A particle moves in one dimension x under the influence of a potential V(x) as
sketched in the figure below. The shaded region corresponds to infinite V, i.e., the
particle is not allowed to penetrate there.
V(x)
a
b
a²Vo =
If there is an energy eigenvalue E = 0, then a and V, are related by
a²Vo =
(n + ² ) ² n²
2m
3-1
n²π²
2m
a²V₁ =
(n + ²) π ²
2m
-Vo
nπ²
0
a
X
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 5 steps with 3 images

Knowledge Booster