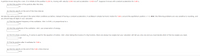
A particle moves along the x axis. It is initially at the position 0.250 m, moving with velocity 0.090 m/s and acceleration -0.430 m/s2. Suppose it moves with constant acceleration for 5.80 s. (a) Find the position of the particle after this time. m (b) Find its velocity at the end of this time interval. m/s We take the same particle and give it the same initial conditions as before. Instead of having a constant acceleration, it oscillates in simple harmonic motion for 5.80 s around the equilibrium position x = 0. Hint: the following problems are very sensitive to rounding, and you should keep all digits in your calculator. (c) Find the angular frequency of the oscillation. Hint: in SHM, a is proportional to x. (d) Find the amplitude of the oscillation. Hint: use conservation of energy. m (e) Find its phase constant . if cosine is used for the equation of motion. Hint: when taking the inverse of a trig function, there are always two angles but your calculator will tell you only one and you must decide which of the two angles you need. rad

Physics Question #61 is the attached image

A particle moves along the x-axis. The velocity of this particle as a function of time is shown in the figure. Assume the particle is located at x = 0 m at time t = 0 s. What is the acceleration of the particle at time t = 26.0 s? What is the position of the particle along the x-axis at time t = 26.0 s? What is the net displacement of the particle between time t = 8.0 s and t = 34.0 s?

Physics A miniature quadcopter is located at x, = 2.25 m and y, =-2.70 m at t = 0 and moves with an average velocity having components Yav, x = 1.70 m/s and Yav, y =-2.50 m/s. What are the x- coordinate and y-coordinate (in m) of the quadcopter's position at t = 1.60 s? x-coordinate = y-coordinate = Please help! Thank you in advance!

A particle moves along the x axis. It is initially at the position 0.240 m, moving with velocity 0.150 m/s and acceleration -0.240 m/s?. Suppose it moves with constant acceleration for 4.80 s. (a) Find the position of the particle after this time. (b) Find its velocity at the end of this time interval. m/s We take the same particle and give it the same initial conditions as before. Instead of having a constant acceleration, it oscillates in simple harmonic motion for 4.80 s around the equilibrium position x = 0. Hint: the following problems are very sensitive to rounding, and you should keep all digits in your calculator. (c) Find the angular frequency of the oscillation. Hint: in SHM, a is proportional to x. /s (d) Find the amplitude of the oscillation. Hint: use conservation of energy. m (e) Find its phase constant e, if cosine is used for the equation of motion. Hint: when taking the inverse of a trig function, there are always two angles but your calculator will tell you only one…

2. The velocity of a particle is given by v = {14t?î+ (4t + 3)j + 6t³k} m/s, where t is in seconds. If the particle is at the origin when t = 0, determine the magnitude of the particle's acceleration when t = 3 s. Also, what is the x, y, z coordinate position of the particle at this instant?

You launch a model rocket from ground level. It moves directly upward with a constant acceleration of 79.0 m/s2 for 1.50 seconds, at which point it runs out of fuel. Assuming air resistance on the rocket is negligible, what is the maximum altitude (above the ground) achieved by the rocket?

Mature salmon swim upstream, returning to spawn at their birthplace. During the arduous trip they leap vertically upward over waterfalls as high as 3.29 m. With what minimum speed (in m/s) must a salmon launch itself into the air to clear a 3.29-m waterfall? HINT