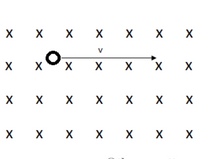
A negative charge of q = -3.1 × 10-17C and m = 2.9 × 10-26 kg enters a magnetic field B = 0.65 T with initial velocity v = 110 m/s, as shown in the figure. The magnetic field points into the screen.
a. Express the magnitude of the magnetic force, F, in terms of q, v, and B.
F=
b. Express the centripetal acceleration of the particle in terms of the force F and the mass m.
a=
c. Express the radius, R, of the circular motion in terms of the centripetal acceleration a and the speed v.
R=
d. Which direction will the magnetic force be on the charge?
| Downward. | To the left. | Into the screen. | Out of the screen. |
| To the right. | Upward. |
e. Under such a magnetic force, which kind of motion will the charge undergo?
|
f. Calculate the magnitude of the force F, in newtons.
F=
g. Calculate the magnitude of a, in meters per square second.
a=
h. Calculate the numerical value of the radius R, in meters.
R=
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps

- A wire of length = 0.35 m is conducting a current of i = 7.5 A toward the top of the page and through a B = 3.0 T uniform magnetic field directed into the page, as shown in the figure. What is the magnitude F of the magnetic force on the wire? F = What is the direction of the magnetic force on the wire? ОО left into the screen up right down out of the screen N Barrow_forwardYou have placed electrons in a magnetic field. The electrons move in horizontal circles of radius 9.5 cm when their speed is 2.0×10^6 m/s. What is the magnitude and direction of the magnetic field that causes this motion?arrow_forwardAn electron moves with velocity v= (7.0i−6.0j)×10^4 m/s in a magnetic field B = (−0.80i+0.60j)T . a. Determine the x -component of the force on the electron. b. Determine the y -component of the force on the electron. c. Determine the z -component of the force on the electron.arrow_forward
- A particle with charge 9.49 x 10^-6 C moves at 1.86 x 10^6 m/s through a magnetic field of strength 2.95 T. The angle between the particle s velocity and the magnetic field direction is 48.3 degrees and the particle undergoes an acceleration of 17.4 m/s^2. What is the particle s mass? 2.23 kg 8.7 kg 15.7 kg 22.6 kgarrow_forwardAn electron in a magnetic field moves along a circle with a radius of 25.4 m with a speed that follows: v(t)=V0e−bt where b = 0.56 s-1and V0 = 170 m/s. I need to find the angular acceleration at t=3.7s, but I don't know how I'm supposed to get that becuase the formula that we have says that it is the second derivative of angular position, but when I calculate angular position all I get is 6.57516 radians. I don't understand how I'm supposed to take a derivative of that since it doesn't have any variables. I don't know if it is needed for this, but I already calculated the centripetal acceleration as 18.0446m/s^2arrow_forwardQ39arrow_forward
- Two particles have the same charge (q1=q23D1.6x10-1C) and different masses undergo circular motion in a constant magnetic field (B = 0.40 T) with the same speed of 5x10° m/s. If their circular paths differ in radius by 4.9 cm, what is the difference in the mass of these two particles? m2 ml a. 8.18 x10^(-28) kg O b. 7.11 x10^(-28) kg Oc 6.27 x10^(-28) kg O d. 5.00 x10^(-28) kg O e. 9.21 x10^(-28) kg G-Guard O Oarrow_forwardA particle with charge q enters a region with a uniform magnetic field Bthat acts in x and z directions (By = 0). The initial velocity of the particle is v = 2î +3ŷ. The force acting on the particle is given by F = q(-3 î + 2ĵ – 9k). Find the magnetic field vector B O a. B= -3î – k O b. B = 3î . O c. B= 2î + 3k O d. B= 4î – 2k O e. B= 2î – 3karrow_forward